Normalverteilung

Normalverteilung
Dichtefunktion 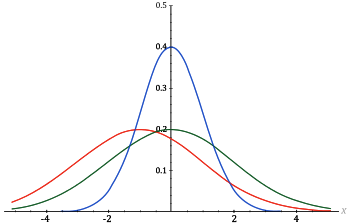Dichtifunkzione vo de Normalverdäilige ${\displaystyle \scriptstyle {\mathcal {N}}(0,1)}$ (blau), ${\displaystyle \scriptstyle {\mathcal {N}}(0,4)}$ (grüen) und ${\displaystyle \scriptstyle {\mathcal {N}}(-1,4)}$ (root)
Verdäiligsfunkzion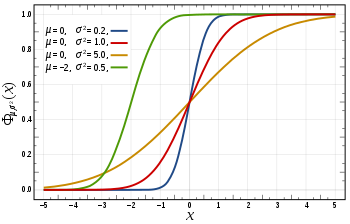 Verdäiligsfunkzione vo de Normalverdäilige ${\displaystyle \scriptstyle {\mathcal {N}}(0,0{.}2)}$ (blau), ${\displaystyle \scriptstyle {\mathcal {N}}(0,1)}$ (root), ${\displaystyle \scriptstyle {\mathcal {N}}(0,5)}$ (gääl) und ${\displaystyle \scriptstyle {\mathcal {N}}(-2,0{.}5)}$ (grüen)
Parameter	μ ∈ R — Erwartigswärt σ2 > 0 — Varianz
Drääger	x ∈ R
Dichdifunkzioon	${\displaystyle {\frac {1}{\sqrt {2\pi \sigma ^{2}}}}\operatorname {exp} \left\{-{\frac {\left(x-\mu \right)^{2}}{2\sigma ^{2}}}\right\}}$
Verdäiligsfunkzioon	${\displaystyle {\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x-\mu }{\sqrt {2\sigma ^{2}}}}\right)\right]}$
Erwardigswärt	μ
Median	μ
Modus	μ
Varianz	${\displaystyle \sigma ^{2}\,}$
Schiefi	0
Wölbig	0
Entropii	${\displaystyle {\frac {1}{2}}\ln(2\pi e\,\sigma ^{2})}$
Momenterzüügendi Funkzion	${\displaystyle \exp \left\{\mu t+{\frac {1}{2}}\sigma ^{2}t^{2}\right\}}$
Charakteristischi Funkzion	${\displaystyle \exp \left\{i\mu t-{\frac {1}{2}}\sigma ^{2}t^{2}\right\}}$
Fisher-Informazioon	${\displaystyle {\begin{pmatrix}1/\sigma ^{2}&0\\0&1/(2\sigma ^{4})\end{pmatrix}}}$

D Normal- oder Gauss-Verdäilig (noch em Carl Friedrich Gauß) isch e wichdige Tüp vo stetige Woorschinlikäitsverdäilige. Iirere Woorschinlikäitsdichdi säit mä au Gauss-Funkzion, d Gauss Normalverdäilig, d Gauss Verdäiligskurve, d Gauss-Kurve, d Gauss Gloggekurve, d Gauss-Glogge oder äifach d Gloggekurve.

Die bsundrigi Bedütig vo dr Normalverdäilig chunnt under anderem vom zentrale Gränzwärtsatz. Noch däm Satz si Verdäilige, wo entstöön, wenn e Hufe unabhängigi Iiflüss überlaageret wärde, under schwache Vorussetzige meer oder weniger normalverdäilt.

D Abwiichige vo de (Mäss)Wärt von e Hufe natur-, wirtschafts- und ääscheniöörwüsseschaftlige Vorgäng vom Middelwärt cha mä mit dr Normalverdäilig (bi biologische Brozäss vilmol e logarithmische Normalverteilung) äntwääder exakt oder wenigstens in ere seer guete Nööcherig beschriibe (vor allem Brozäss, wo in meerere Faktore unabhängig vonenander in verschiidene Richdige wirke).

Zuefallsgröössene mit Normalverdäilig benützt mä zum zuefelligi Vorgäng beschriibe wie:

• zuefelligi Mässfeeler,
• zuefelligi Abwiichige vom Nennmaass bi dr Brodukzioon vo Wärkstück,
• Beschriibig vo dr brownsche Molekularbeweegig.

In dr Versicherigsmathematik isch d Normalverdäilig geignet zum e Modäll mache vo de Daate vo Schääde im Beriich vo dr middlere Hööchi vom Schaade.

In dr Mässtechnik setzt mä hüfig e Normalverdäilig aa, wo d Ströijig vo de Mässfeeler beschribt. Do isch s wichdig, wie vil Mässpünggt innerhalb von ere gwüsse Ströibräiti lige.

D Standardabwiichig ${\displaystyle \sigma }$ beschribt d Bräiti vo dr Normalverdäilig. D Halbwärtbräiti von ere gauss-artige Verdäilig isch öbbe s 2,4-fache (genau ${\displaystyle 2{\sqrt {2\ln 2}}}$) vo dr Standardabwiichig. Es gältet nööcherigswiis:

• Im Interwall vo dr Abwiichig ${\displaystyle \pm \sigma }$ vom Middelwärt findet mä 68,27 % vo alle Mässwärt,
• Im Interwall vo dr Abwiichig ${\displaystyle \pm 2\sigma }$ vom Middelwärt findet mä 95,45 % vo alle Mässwärt,
• Im Interwall vo dr Abwiichig ${\displaystyle \pm 3\sigma }$ vom Middelwärt findet mä 99,73 % vo alle Mässwärt.

Umkeert cha mä für Woorschinlikäite, wo gee si, die maximale Abwiichige vom Middelwärt finde:

• 50 % vo alle Mässwärt häi e Abwiichig vo höggstens ${\displaystyle 0{,}675\sigma }$ vom Middelwärt,
• 90 % vo alle Mässwärt häi e Abwiichig vo höggstens ${\displaystyle 1{,}645\sigma }$ vom Middelwärt,
• 95 % vo alle Mässwärt häi e Abwiichig vo höggstens ${\displaystyle 1{,}960\sigma }$ vom Middelwärt,
• 99 % vo alle Mässwärt häi e Abwiichig vo höggstens ${\displaystyle 2{,}576\sigma }$ vom Middelwärt.

Mä cha eso näben em Middelwärt au dr Standardabwiichig en äifachi Bedütig zueordne.