Anhemitonic scale

For scales with three notes, see Tritonic scale.
{ \override Score.TimeSignature #'stencil = ##f \relative c' { \clef treble \key c \major \time 6/4 d f g a c d } }
Min'yō scale on D,[1] equivalent to yo scale on C,[2] an anhemitonic scale
{ \override Score.TimeSignature #'stencil = ##f \relative c' { \clef treble \key c \major \time 6/4 d ees g a bes d } }
Miyako-bushi scale on D, equivalent to in scale on D,[3] a hemitonic scale

Musicology commonly classifies scales as either hemitonic or anhemitonic. Hemitonic scales contain one or more semitones, while anhemitonic scales do not contain semitones. For example, in traditional Japanese music, the anhemitonic yo scale is contrasted with the hemitonic in scale.[4] The simplest and most commonly used scale in the world is the atritonic anhemitonic "major" pentatonic scale. The whole tone scale is also anhemitonic.

{ \override Score.TimeSignature #'stencil = ##f \relative c' { \clef treble \key c \major \time 7/4 c d ees fis g aes b c } }
Hungarian minor scale on C, a cohemitonic scale.[5]

A special subclass of the hemitonic scales is the cohemitonic scales.[6] Cohemitonic scales contain two or more semitones (making them hemitonic) such that two or more of the semitones appear consecutively in scale order. For example, the Hungarian minor scale in C includes F♯, G, and A♭ in that order, with a semitone between F♯ and G, and then a semitone between G and A♭.

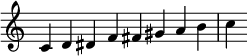
{ \override Score.TimeSignature #'stencil = ##f \relative c' { \clef treble \key c \major \time 8/4 c d dis f fis gis a b c } }
{ \override Score.TimeSignature #'stencil = ##f \relative c' { \clef treble \key c \major \time 8/4 c des ees e ges g a bes c } }
Octatonic scales on C, hemitonic but ancohemitonic

Ancohemitonic scales, in contrast, either contain no semitones (and thus are anhemitonic), or contain semitones (being hemitonic) where none of the semitones appear consecutively in scale order.[7][failed verification] Some authors, however, do not include anhemitonic scales in their definition of ancohemitonic scales. Examples of ancohemitonic scales are numerous, as ancohemitonia is favored over cohemitonia in the world's musics: diatonic scale, melodic major/melodic minor, harmonic major scale, harmonic minor scale, Hungarian major scale, Romanian major scale, and the so-called octatonic scale.

Hemitonia is also quantified by the number of semitones present. Unhemitonic scales have only one semitone; dihemitonic scales have 2 semitones; trihemitonic scales have 3 semitones, etc. In the same way that an anhemitonic scale is less dissonant than a hemitonic scale, an anhemitonic scale is less dissonant than a dihemitonic scale.

The qualification of cohemitonia versus ancohemitonia combines with the cardinality of semitones, giving terms like: dicohemitonic, triancohemitonic, and so forth. An ancohemitonic scale is less dissonant than a cohemitonic scale, the count of their semitones being equal. In general, the number of semitones is more important to the perception of dissonance than the adjacency (or lack thereof) of any pair of them. Additional adjacency between semitones (once adjacency is present) does not necessarily increase the dissonance, the count of semitones again being equal.[8]

Related to these semitone classifications are tritonic and atritonic scales. Tritonic scales contain one or more tritones, while atritonic scales do not contain tritones. A special monotonic relationship exists between semitones and tritones as scales are built by projection, q.v. below.

The harmonic relationship of all these categories comes from the perception that semitones and tritones are the severest of dissonances, and that avoiding them is often desirable. The most-used scales across the planet are anhemitonic. Of the remaining hemitonic scales, the ones most used are ancohemitonic.

  1. ^ Susan Miyo Asai (1999). Nōmai Dance Drama, p. 126. ISBN 978-0-313-30698-3.
  2. ^ Minoru Miki, Marty Regan, Philip Flavin (2008). Composing for Japanese instruments, p. 2. ISBN 978-1-58046-273-0.
  3. ^ Titon, Jeff Todd (1996). Worlds of Music: An Introduction to the Music of the World's Peoples, p. 373. ISBN 0-02-872612-X.
  4. ^ Anon. (2001) "Ditonus", The New Grove Dictionary of Music and Musicians, second edition, edited by Stanley Sadie and John Tyrrell. London: Macmillan Publishers; Bence Szabolcsi (1943), "Five-Tone Scales and Civilization", Acta Musicologica 15, Fasc. 1/4 (January–December): pp. 24–34, citation on p. 25.
  5. ^ Kahan, Sylvia (2009). In Search of New Scales, p. 39. ISBN 978-1-58046-305-8. Cites Liszt. Des Bohémians, p. 301.
  6. ^ Christ, William (1966). Materials and Structure of Music, v.1, p. 39. Englewood Cliffs: Prentice–Hall. LOC 66-14354.
  7. ^ Tymoczko, Dmitri (1997). "The Consecutive-Semitone Constraint on Scalar Structure: A Link between Impressionism and Jazz", Intégral, v.11, (1997), p. 135-179.
  8. ^ Keith, Michael. 1991. From Polychords to Polya : Adventures in Musical Combinatorics, p. 45. Princeton: Vinculum Press. ISBN 978-0963009708.