Apeirogonal antiprism

Uniform apeirogonal antiprism
Type	Semiregular tiling
Vertex configuration	3.3.3.∞
Schläfli symbol	sr{2,∞} or ${\displaystyle s{\begin{Bmatrix}\infty \\2\end{Bmatrix}}}$
Wythoff symbol	| 2 2 ∞
Coxeter diagram
Symmetry	[∞,2+], (∞22)
Rotation symmetry	[∞,2]+, (∞22)
Bowers acronym	Azap
Dual	Apeirogonal deltohedron
Properties	Vertex-transitive

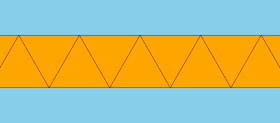
In geometry, an apeirogonal antiprism or infinite antiprism^[1] is the arithmetic limit of the family of antiprisms; it can be considered an infinite polyhedron or a tiling of the plane.

If the sides are equilateral triangles, it is a uniform tiling. In general, it can have two sets of alternating congruent isosceles triangles, surrounded by two half-planes.