
| Language or processor | Left | Right |
|---|---|---|
| ActionScript 3, Java, JavaScript, Python, PHP, Ruby, C, C++,[1]D, C#, Go, Julia, Rust (signed types only)[2], Swift (signed types only)[note 1] |
<< |
>>
|
| Ada | Shift_Left [3] |
Shift_Right_Arithmetic
|
| Kotlin | shl |
shr
|
| Fortran | SHIFTL |
SHIFTA [note 2]
|
| Standard ML | << |
~>>
|
| Verilog | <<< |
>>> [note 3]
|
| OpenVMS macro language | @[note 4] | |
| Scheme | arithmetic-shift[note 5]
| |
| Common Lisp | ash
| |
| OCaml | lsl |
asr
|
| Haskell | Data.Bits.shift[note 6]
| |
| VHDL | sla[note 7] |
sra
|
| Assembly: Z80 | SLA[5] |
SRA
|
| Assembly: x86 | SAL |
SAR
|
| Assembly: 68k | ASL |
ASR
|
| Assembly: RISC-V | sll, slli[6] |
sra, srai
|
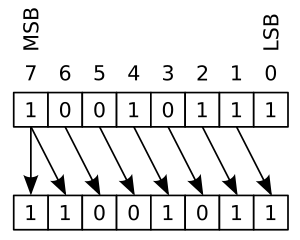
In computer programming, an arithmetic shift is a shift operator, sometimes termed a signed shift (though it is not restricted to signed operands). The two basic types are the arithmetic left shift and the arithmetic right shift. For binary numbers it is a bitwise operation that shifts all of the bits of its operand; every bit in the operand is simply moved a given number of bit positions, and the vacant bit-positions are filled in. Instead of being filled with all 0s, as in logical shift, when shifting to the right, the leftmost bit (usually the sign bit in signed integer representations) is replicated to fill in all the vacant positions (this is a kind of sign extension).
Some authors prefer the terms sticky right-shift and zero-fill right-shift for arithmetic and logical shifts respectively.[7]
Arithmetic shifts can be useful as efficient ways to perform multiplication or division of signed integers by powers of two. Shifting left by n bits on a signed or unsigned binary number has the effect of multiplying it by 2n. Shifting right by n bits on a two's complement signed binary number has the effect of dividing it by 2n, but it always rounds down (towards negative infinity). This is different from the way rounding is usually done in signed integer division (which rounds towards 0). This discrepancy has led to bugs in a number of compilers.[8]
For example, in the x86 instruction set, the SAR instruction (arithmetic right shift) divides a signed number by a power of two, rounding towards negative infinity.[9] However, the IDIV instruction (signed divide) divides a signed number, rounding towards zero. So a SAR instruction cannot be substituted for an IDIV by power of two instruction nor vice versa.
- ^ "Bit manipulation - Dlang Tour". tour.dlang.org. Retrieved 2019-06-23.
- ^ "Operator Expressions: Arithmetic and Logical Binary Operators". doc.rust-lang.org. Retrieved 2022-11-13.
- ^ "Annotated Ada 2012 Reference Manual".
- ^ HP 2001.
- ^ "Z80 Assembler Syntax".
- ^ "The RISC-V Instruction Set Manual, Volume I: Unprivileged ISA" (PDF). GitHub. 2019-12-13. pp. 18–20. Archived (PDF) from the original on 2022-10-09. Retrieved 2021-08-07.
- ^ Thomas R. Cain and Alan T. Sherman. "How to break Gifford's cipher". Section 8.1: "Sticky versus Non-Sticky Bit-shifting". Cryptologia. 1997.
- ^ Steele Jr, Guy. "Arithmetic Shifting Considered Harmful" (PDF). MIT AI Lab. Archived (PDF) from the original on 2022-10-09. Retrieved 20 May 2013.
- ^ Hyde 1996, § 6.6.2.2 SAR.
Cite error: There are <ref group=note> tags on this page, but the references will not show without a {{reflist|group=note}} template (see the help page).