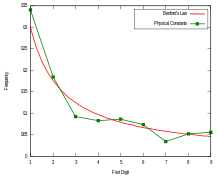
Benford's law

Not to be confused with the unrelated adage Benford's law of controversy.
A sequence of decreasing blue bars against a light gray grid background
The distribution of first digits, according to Benford's law. Each bar represents a digit, and the height of the bar is the percentage of numbers that start with that digit.
Frequency of first significant digit of physical constants plotted against Benford's law

Benford's law, also known as the Newcomb–Benford law, the law of anomalous numbers, or the first-digit law, is an observation that in many real-life sets of numerical data, the leading digit is likely to be small.[1] In sets that obey the law, the number 1 appears as the leading significant digit about 30% of the time, while 9 appears as the leading significant digit less than 5% of the time. Uniformly distributed digits would each occur about 11.1% of the time.[2] Benford's law also makes predictions about the distribution of second digits, third digits, digit combinations, and so on.

The graph to the right shows Benford's law for base 10, one of infinitely many cases of a generalized law regarding numbers expressed in arbitrary (integer) bases, which rules out the possibility that the phenomenon might be an artifact of the base-10 number system. Further generalizations published in 1995[3] included analogous statements for both the nth leading digit and the joint distribution of the leading n digits, the latter of which leads to a corollary wherein the significant digits are shown to be a statistically dependent quantity.

It has been shown that this result applies to a wide variety of data sets, including electricity bills, street addresses, stock prices, house prices, population numbers, death rates, lengths of rivers, and physical and mathematical constants.[4] Like other general principles about natural data—for example, the fact that many data sets are well approximated by a normal distribution—there are illustrative examples and explanations that cover many of the cases where Benford's law applies, though there are many other cases where Benford's law applies that resist simple explanations.[5][6] Benford's law tends to be most accurate when values are distributed across multiple orders of magnitude, especially if the process generating the numbers is described by a power law (which is common in nature).

The law is named after physicist Frank Benford, who stated it in 1938 in an article titled "The Law of Anomalous Numbers",[7] although it had been previously stated by Simon Newcomb in 1881.[8][9]

The law is similar in concept, though not identical in distribution, to Zipf's law.

  1. ^ Arno Berger and Theodore P. Hill, Benford's Law Strikes Back: No Simple Explanation in Sight for Mathematical Gem, 2011.
  2. ^ Weisstein, Eric W. "Benford's Law". MathWorld, A Wolfram web resource. Retrieved 7 June 2015.
  3. ^ Hill, Theodore (1995). "A Statistical Derivation of the Significant-Digit Law". Statistical Science. 10 (4). doi:10.1214/ss/1177009869.
  4. ^ Paul H. Kvam, Brani Vidakovic, Nonparametric Statistics with Applications to Science and Engineering, p. 158.
  5. ^ Berger, Arno; Hill, Theodore P. (30 June 2020). "The mathematics of Benford's law: a primer". Stat. Methods Appl. 30 (3): 779–795. arXiv:1909.07527. doi:10.1007/s10260-020-00532-8. S2CID 202583554.
  6. ^ Cai, Zhaodong; Faust, Matthew; Hildebrand, A. J.; Li, Junxian; Zhang, Yuan (15 March 2020). "The Surprising Accuracy of Benford's Law in Mathematics". The American Mathematical Monthly. 127 (3): 217–237. arXiv:1907.08894. doi:10.1080/00029890.2020.1690387. ISSN 0002-9890. S2CID 198147766.
  7. ^ Frank Benford (March 1938). "The law of anomalous numbers". Proc. Am. Philos. Soc. 78 (4): 551–572. Bibcode:1938PAPhS..78..551B. JSTOR 984802.
  8. ^ Cite error: The named reference Newcomb was invoked but never defined (see the help page).
  9. ^ Cite error: The named reference Formann2010 was invoked but never defined (see the help page).