| Bitruncated cubic honeycomb | |
|---|---|
 
| |
| Type | Uniform honeycomb |
| Schläfli symbol | 2t{4,3,4} t1,2{4,3,4} |
| Coxeter-Dynkin diagram | |
| Cell type | (4.6.6) |
| Face types | square {4} hexagon {6} |
| Edge figure | isosceles triangle {3} |
| Vertex figure | 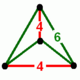 (tetragonal disphenoid) |
| Space group Fibrifold notation Coxeter notation |
Im3m (229) 8o:2 [[4,3,4]] |
| Coxeter group | , [4,3,4] |
| Dual | Oblate tetrahedrille Disphenoid tetrahedral honeycomb Cell: 
|
| Properties | isogonal, isotoxal, isochoric |

The bitruncated cubic honeycomb is a space-filling tessellation (or honeycomb) in Euclidean 3-space made up of truncated octahedra (or, equivalently, bitruncated cubes). It has 4 truncated octahedra around each vertex. Being composed entirely of truncated octahedra, it is cell-transitive. It is also edge-transitive, with 2 hexagons and one square on each edge, and vertex-transitive. It is one of 28 uniform honeycombs.
John Horton Conway calls this honeycomb a truncated octahedrille in his Architectonic and catoptric tessellation list, with its dual called an oblate tetrahedrille, also called a disphenoid tetrahedral honeycomb. Although a regular tetrahedron can not tessellate space alone, this dual has identical disphenoid tetrahedron cells with isosceles triangle faces.
