Butterfly effect

For other uses, see Butterfly effect (disambiguation).
A plot of Lorenz' strange attractor for values ρ=28, σ = 10, β = 8/3. The butterfly effect or sensitive dependence on initial conditions is the property of a dynamical system that, starting from any of various arbitrarily close alternative initial conditions on the attractor, the iterated points will become arbitrarily spread out from each other.
Experimental demonstration of the butterfly effect with six recordings of the same double pendulum. In each recording, the pendulum starts with almost the same initial condition. Over time, the differences in the dynamics grow from almost unnoticeable to drastic.

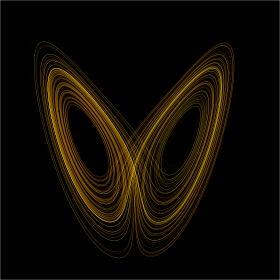
In chaos theory, the butterfly effect is the sensitive dependence on initial conditions in which a small change in one state of a deterministic nonlinear system can result in large differences in a later state.

The term is closely associated with the work of the mathematician and meteorologist Edward Norton Lorenz. He noted that the butterfly effect is derived from the example of the details of a tornado (the exact time of formation, the exact path taken) being influenced by minor perturbations such as a distant butterfly flapping its wings several weeks earlier. Lorenz originally used a seagull causing a storm but was persuaded to make it more poetic with the use of a butterfly and tornado by 1972.[1][2] He discovered the effect when he observed runs of his weather model with initial condition data that were rounded in a seemingly inconsequential manner. He noted that the weather model would fail to reproduce the results of runs with the unrounded initial condition data. A very small change in initial conditions had created a significantly different outcome.[3]

The idea that small causes may have large effects in weather was earlier acknowledged by the French mathematician and physicist Henri Poincaré. The American mathematician and philosopher Norbert Wiener also contributed to this theory. Lorenz's work placed the concept of instability of the Earth's atmosphere onto a quantitative base and linked the concept of instability to the properties of large classes of dynamic systems which are undergoing nonlinear dynamics and deterministic chaos.[4]

The concept of the butterfly effect has since been used outside the context of weather science as a broad term for any situation where a small change is supposed to be the cause of larger consequences.

  1. ^ "Predictability: Does the Flap of a Butterfly's Wings in Brazil Set Off a Tornado in Texas?" (PDF). Archived (PDF) from the original on 2022-10-09. Retrieved 23 December 2021.
  2. ^ "When Lorenz Discovered the Butterfly Effect". 22 May 2015. Retrieved 23 December 2021.
  3. ^ Lorenz, Edward N. (March 1963). "Deterministic Nonperiodic Flow". Journal of the Atmospheric Sciences. 20 (2): 130–141. Bibcode:1963JAtS...20..130L. doi:10.1175/1520-0469(1963)020<0130:dnf>2.0.co;2.
  4. ^ Rouvas-Nicolis, Catherine; Nicolis, Gregoire (4 May 2009). "Butterfly effect". Scholarpedia. Vol. 4. p. 1720. Bibcode:2009SchpJ...4.1720R. doi:10.4249/scholarpedia.1720. Archived from the original on 2016-01-02. Retrieved 2016-01-02.