Cage (graph theory)

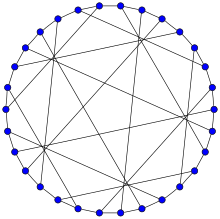
In the mathematical field of graph theory, a cage is a regular graph that has as few vertices as possible for its girth.

Formally, an $(r, g)$ -graph is defined to be a graph in which each vertex has exactly $r$ neighbors, and in which the shortest cycle has length exactly $g$ . An $(r, g)$ -cage is an $(r, g)$ -graph with the smallest possible number of vertices, among all $(r, g)$ -graphs. A $(3, g)$ -cage is often called a $g$ -cage.

It is known that an $(r, g)$ -graph exists for any combination of $r \geq 2$ and $g \geq 3$ . It follows that all $(r, g)$ -cages exist.

If a Moore graph exists with degree $r$ and girth $g$ , it must be a cage. Moreover, the bounds on the sizes of Moore graphs generalize to cages: any cage with odd girth $g$ must have at least

1+r\sum _{i=0}^{(g-3)/2}(r-1)^{i}

vertices, and any cage with even girth $g$ must have at least

2\sum _{i=0}^{(g-2)/2}(r-1)^{i}

vertices. Any $(r, g)$ -graph with exactly this many vertices is by definition a Moore graph and therefore automatically a cage.

There may exist multiple cages for a given combination of $r$ and $g$ . For instance there are three non-isomorphic $(3, 10)$ -cages, each with 70 vertices: the Balaban 10-cage, the Harries graph and the Harries–Wong graph. But there is only one $(3, 11)$ -cage: the Balaban 11-cage (with 112 vertices).