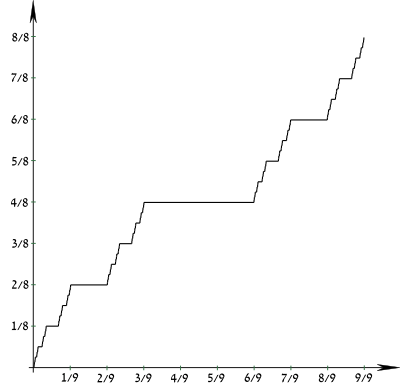
In mathematics, the Cantor function is an example of a function that is continuous, but not absolutely continuous. It is a notorious counterexample in analysis, because it challenges naive intuitions about continuity, derivative, and measure. Though it is continuous everywhere and has zero derivative almost everywhere, its value still goes from 0 to 1 as its argument reaches from 0 to 1. Thus, in one sense the function seems very much like a constant one which cannot grow, and in another, it does indeed monotonically grow.
It is also called the Cantor ternary function, the Lebesgue function,[1] Lebesgue's singular function, the Cantor–Vitali function, the Devil's staircase,[2] the Cantor staircase function,[3] and the Cantor–Lebesgue function.[4] Georg Cantor (1884) introduced the Cantor function and mentioned that Scheeffer pointed out that it was a counterexample to an extension of the fundamental theorem of calculus claimed by Harnack. The Cantor function was discussed and popularized by Scheeffer (1884), Lebesgue (1904) and Vitali (1905).
- ^ Vestrup 2003, Section 4.6.
- ^ Thomson, Bruckner & Bruckner 2008, p. 252.
- ^ "Cantor Staircase Function".
- ^ Bass 2013, p. 28.