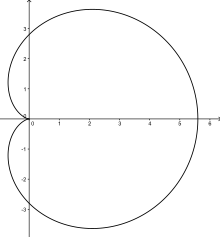

In geometry, a cardioid (from Greek καρδιά (kardiá) 'heart') is a plane curve traced by a point on the perimeter of a circle that is rolling around a fixed circle of the same radius. It can also be defined as an epicycloid having a single cusp. It is also a type of sinusoidal spiral, and an inverse curve of the parabola with the focus as the center of inversion.[1] A cardioid can also be defined as the set of points of reflections of a fixed point on a circle through all tangents to the circle.[2]
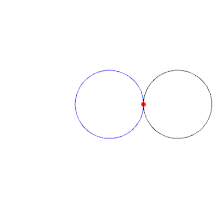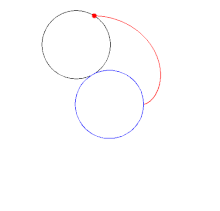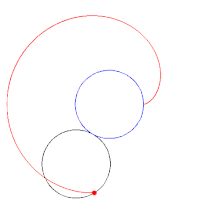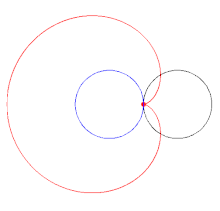
The name was coined by Giovanni Salvemini in 1741[3] but the cardioid had been the subject of study decades beforehand.[4] Although named for its heart-like form, it is shaped more like the outline of the cross-section of a round apple without the stalk.[5]
A cardioid microphone exhibits an acoustic pickup pattern that, when graphed in two dimensions, resembles a cardioid (any 2d plane containing the 3d straight line of the microphone body). In three dimensions, the cardioid is shaped like an apple centred around the microphone which is the "stalk" of the apple.
- ^ Weisstein, Eric W. "Parabola Inverse Curve". MathWorld.
- ^ S Balachandra Rao . Differential Calculus, p. 457
- ^ Lockwood
- ^ Yates
- ^ Gutenmacher, Victor; Vasilyev, N. B. (2004). Lines and Curves. Boston: Birkhäuser. p. 90. doi:10.1007/978-1-4757-3809-4. ISBN 9781475738094.