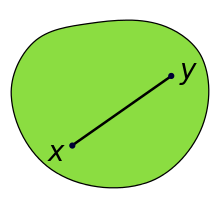

In geometry, a set of points is convex if it contains every line segment between two points in the set. Equivalently, a convex set or a convex region is a set that intersects every line in a line segment, single point, or the empty set.[1][2] For example, a solid cube is a convex set, but anything that is hollow or has an indent, for example, a crescent shape, is not convex.
The boundary of a convex set in the plane is always a convex curve. The intersection of all the convex sets that contain a given subset A of Euclidean space is called the convex hull of A. It is the smallest convex set containing A.
A convex function is a real-valued function defined on an interval with the property that its epigraph (the set of points on or above the graph of the function) is a convex set. Convex minimization is a subfield of optimization that studies the problem of minimizing convex functions over convex sets. The branch of mathematics devoted to the study of properties of convex sets and convex functions is called convex analysis.
Spaces in which convex sets are defined include the Euclidean spaces, the affine spaces over the real numbers, and certain non-Euclidean geometries. The notion of a convex set in Euclidean spaces can be generalized in several ways by modifying its definition, for instance by restricting the line segments that such a set is required to contain.
- ^ Morris, Carla C.; Stark, Robert M. (24 August 2015). Finite Mathematics: Models and Applications. John Wiley & Sons. p. 121. ISBN 9781119015383. Retrieved 5 April 2017.
- ^ Kjeldsen, Tinne Hoff. "History of Convexity and Mathematical Programming" (PDF). Proceedings of the International Congress of Mathematicians (ICM 2010): 3233–3257. doi:10.1142/9789814324359_0187. Archived from the original (PDF) on 2017-08-11. Retrieved 5 April 2017.