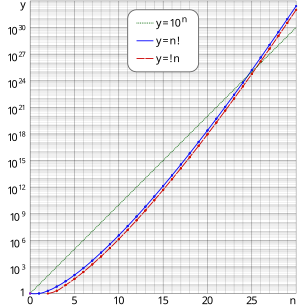
| Table of values | |||
|---|---|---|---|
| Permutations, | Derangements, | ||
| 0 | 1 =1×100 | 1 =1×100 | = 1 |
| 1 | 1 =1×100 | 0 | = 0 |
| 2 | 2 =2×100 | 1 =1×100 | = 0.5 |
| 3 | 6 =6×100 | 2 =2×100 | ≈0.33333 33333 |
| 4 | 24 =2.4×101 | 9 =9×100 | = 0.375 |
| 5 | 120 =1.20×102 | 44 =4.4×101 | ≈0.36666 66667 |
| 6 | 720 =7.20×102 | 265 =2.65×102 | ≈0.36805 55556 |
| 7 | 5,040 =5.04×103 | 1,854 ≈1.85×103 | ≈0.36785,71429 |
| 8 | 40,320 ≈4.03×104 | 14,833 ≈1.48×104 | ≈0.36788 19444 |
| 9 | 362,880 ≈3.63×105 | 133,496 ≈1.33×105 | ≈0.36787 91887 |
| 10 | 3,628,800 ≈3.63×106 | 1,334,961 ≈1.33×106 | ≈0.36787 94643 |
| 11 | 39,916,800 ≈3.99×107 | 14,684,570 ≈1.47×107 | ≈0.36787 94392 |
| 12 | 479,001,600 ≈4.79×108 | 176,214,841 ≈1.76×108 | ≈0.36787 94413 |
| 13 | 6,227,020,800 ≈6.23×109 | 2,290,792,932 ≈2.29×109 | ≈0.36787 94412 |
| 14 | 87,178,291,200 ≈8.72×1010 | 32,071,101,049 ≈3.21×1010 | ≈0.36787 94412 |
| 15 | 1,307,674,368,000 ≈1.31×1012 | 481,066,515,734 ≈4.81×1011 | ≈0.36787 94412 |
| 16 | 20,922,789,888,000 ≈2.09×1013 | 7,697,064,251,745 ≈7.70×1012 | ≈0.36787 94412 |
| 17 | 355,687,428,096,000 ≈3.56×1014 | 130,850,092,279,664 ≈1.31×1014 | ≈0.36787 94412 |
| 18 | 6,402,373,705,728,000 ≈6.40×1015 | 2,355,301,661,033,953 ≈2.36×1015 | ≈0.36787 94412 |
| 19 | 121,645,100,408,832,000 ≈1.22×1017 | 44,750,731,559,645,106 ≈4.48×1016 | ≈0.36787 94412 |
| 20 | 2,432,902,008,176,640,000 ≈2.43×1018 | 895,014,631,192,902,121 ≈8.95×1017 | ≈0.36787 94412 |
| 21 | 51,090,942,171,709,440,000 ≈5.11×1019 | 18,795,307,255,050,944,540 ≈1.88×1019 | ≈0.36787 94412 |
| 22 | 1,124,000,727,777,607,680,000 ≈1.12×1021 | 413,496,759,611,120,779,881 ≈4.13×1020 | ≈0.36787 94412 |
| 23 | 25,852,016,738,884,976,640,000 ≈2.59×1022 | 9,510,425,471,055,777,937,262 ≈9.51×1021 | ≈0.36787 94412 |
| 24 | 620,448,401,733,239,439,360,000 ≈6.20×1023 | 228,250,211,305,338,670,494,289 ≈2.28×1023 | ≈0.36787 94412 |
| 25 | 15,511,210,043,330,985,984,000,000 ≈1.55×1025 | 5,706,255,282,633,466,762,357,224 ≈5.71×1024 | ≈0.36787 94412 |
| 26 | 403,291,461,126,605,635,584,000,000 ≈4.03×1026 | 148,362,637,348,470,135,821,287,825 ≈1.48×1026 | ≈0.36787 94412 |
| 27 | 10,888,869,450,418,352,160,768,000,000 ≈1.09×1028 | 4,005,791,208,408,693,667,174,771,274 ≈4.01×1027 | ≈0.36787 94412 |
| 28 | 304,888,344,611,713,860,501,504,000,000 ≈3.05×1029 | 112,162,153,835,443,422,680,893,595,673 ≈1.12×1029 | ≈0.36787 94412 |
| 29 | 8,841,761,993,739,701,954,543,616,000,000 ≈8.84×1030 | 3,252,702,461,227,859,257,745,914,274,516 ≈3.25×1030 | ≈0.36787 94412 |
| 30 | 265,252,859,812,191,058,636,308,480,000,000 ≈2.65×1032 | 97,581,073,836,835,777,732,377,428,235,481 ≈9.76×1031 | ≈0.36787 94412 |
In combinatorial mathematics, a derangement is a permutation of the elements of a set in which no element appears in its original position. In other words, a derangement is a permutation that has no fixed points.
The number of derangements of a set of size n is known as the subfactorial of n or the n-th derangement number or n-th de Montmort number (after Pierre Remond de Montmort). Notations for subfactorials in common use include !n, Dn, dn, or n¡.[1][2]
For n > 0, the subfactorial !n equals the nearest integer to n!/e, where n! denotes the factorial of n and e is Euler's number.[3]
The problem of counting derangements was first considered by Pierre Raymond de Montmort in his Essay d'analyse sur les jeux de hazard.[4] in 1708; he solved it in 1713, as did Nicholas Bernoulli at about the same time.
- ^ The name "subfactorial" originates with William Allen Whitworth; see Cajori, Florian (2011), A History of Mathematical Notations: Two Volumes in One, Cosimo, Inc., p. 77, ISBN 9781616405717.
- ^ Ronald L. Graham, Donald E. Knuth, Oren Patashnik, Concrete Mathematics (1994), Addison–Wesley, Reading MA. ISBN 0-201-55802-5
- ^ Cite error: The named reference
Hassani2003was invoked but never defined (see the help page). - ^ de Montmort, P. R. (1708). Essay d'analyse sur les jeux de hazard. Paris: Jacque Quillau. Seconde Edition, Revue & augmentée de plusieurs Lettres. Paris: Jacque Quillau. 1713.



