In projective geometry, Desargues's theorem, named after Girard Desargues, states:
- Two triangles are in perspective axially if and only if they are in perspective centrally.
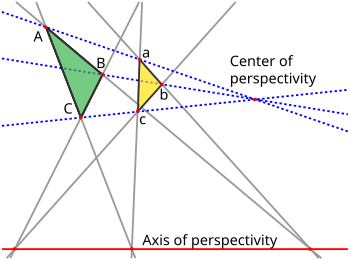
Denote the three vertices of one triangle by a, b and c, and those of the other by A, B and C. Axial perspectivity means that lines ab and AB meet in a point, lines ac and AC meet in a second point, and lines bc and BC meet in a third point, and that these three points all lie on a common line called the axis of perspectivity. Central perspectivity means that the three lines Aa, Bb and Cc are concurrent, at a point called the center of perspectivity.
This intersection theorem is true in the usual Euclidean plane but special care needs to be taken in exceptional cases, as when a pair of sides are parallel, so that their "point of intersection" recedes to infinity. Commonly, to remove these exceptions, mathematicians "complete" the Euclidean plane by adding points at infinity, following Jean-Victor Poncelet. This results in a projective plane.
Desargues's theorem is true for the real projective plane and for any projective space defined arithmetically from a field or division ring; that includes any projective space of dimension greater than two or in which Pappus's theorem holds. However, there are many "non-Desarguesian planes", in which Desargues's theorem is false.