In physics, a dipole (from Ancient Greek δίς (dís) 'twice' and πόλος (pólos) 'axis')[1][2][3] is an electromagnetic phenomenon which occurs in two ways:
- An electric dipole deals with the separation of the positive and negative electric charges found in any electromagnetic system. A simple example of this system is a pair of charges of equal magnitude but opposite sign separated by some typically small distance. (A permanent electric dipole is called an electret.)
- A magnetic dipole is the closed circulation of an electric current system. A simple example is a single loop of wire with constant current through it. A bar magnet is an example of a magnet with a permanent magnetic dipole moment.[4][5]
Dipoles, whether electric or magnetic, can be characterized by their dipole moment, a vector quantity. For the simple electric dipole, the electric dipole moment points from the negative charge towards the positive charge, and has a magnitude equal to the strength of each charge times the separation between the charges. (To be precise: for the definition of the dipole moment, one should always consider the "dipole limit", where, for example, the distance of the generating charges should converge to 0 while simultaneously, the charge strength should diverge to infinity in such a way that the product remains a positive constant.)
For the magnetic (dipole) current loop, the magnetic dipole moment points through the loop (according to the right hand grip rule), with a magnitude equal to the current in the loop times the area of the loop.
Similar to magnetic current loops, the electron particle and some other fundamental particles have magnetic dipole moments, as an electron generates a magnetic field identical to that generated by a very small current loop. However, an electron's magnetic dipole moment is not due to a current loop, but to an intrinsic property of the electron.[6] The electron may also have an electric dipole moment though such has yet to be observed (see electron electric dipole moment).

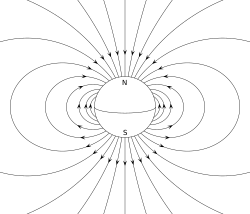
A permanent magnet, such as a bar magnet, owes its magnetism to the intrinsic magnetic dipole moment of the electron. The two ends of a bar magnet are referred to as poles (not to be confused with monopoles, see Classification below) and may be labeled "north" and "south". In terms of the Earth's magnetic field, they are respectively "north-seeking" and "south-seeking" poles: if the magnet were freely suspended in the Earth's magnetic field, the north-seeking pole would point towards the north and the south-seeking pole would point towards the south. The dipole moment of the bar magnet points from its magnetic south to its magnetic north pole. In a magnetic compass, the north pole of a bar magnet points north. However, that means that Earth's geomagnetic north pole is the south pole (south-seeking pole) of its dipole moment and vice versa.
The only known mechanisms for the creation of magnetic dipoles are by current loops or quantum-mechanical spin since the existence of magnetic monopoles has never been experimentally demonstrated.
- ^ δίς, Henry George Liddell, Robert Scott, A Greek-English Lexicon, on Perseus
- ^ πόλος, Henry George Liddell, Robert Scott, A Greek-English Lexicon, on Perseus
- ^ "dipole, n.". Oxford English Dictionary (2nd ed.). Oxford University Press. 1989.
- ^ Brau, Charles A. (2004). Modern Problems in Classical Electrodynamics. Oxford University Press. ISBN 0-19-514665-4.
- ^ Griffiths, David J. (1999). Introduction to Electrodynamics (3rd ed.). Prentice Hall. ISBN 0-13-805326-X.
- ^ Griffiths, David J. (1994). Introduction to Quantum Mechanics. Prentice Hall. ISBN 978-0-13-124405-4.