Probability distribution
Dirichlet distribution|
Probability density function 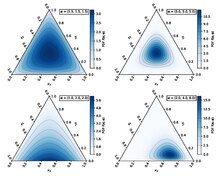 |
| Parameters |
 number of categories (integer) number of categories (integer)
 concentration parameters, where concentration parameters, where  |
|---|
| Support |
 where where ![{\displaystyle x_{i}\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a32830173af0dc0eaf16f580cc75ef2f78b4f15e) and and  |
|---|
| PDF |

where 
where  |
|---|
| Mean |
![{\displaystyle \operatorname {E} [X_{i}]={\frac {\alpha _{i}}{\alpha _{0}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dbec98ee7aeb59af97828e7b3e9fa92de937021d)
![{\displaystyle \operatorname {E} [\ln X_{i}]=\psi (\alpha _{i})-\psi (\alpha _{0})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a864ba2186ba3577dcd095b6b3f608511c668b53)
(where  is the digamma function) is the digamma function) |
|---|
| Mode |
 |
|---|
| Variance |
![{\displaystyle \operatorname {Var} [X_{i}]={\frac {{\tilde {\alpha }}_{i}(1-{\tilde {\alpha }}_{i})}{\alpha _{0}+1}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74281baf02f79a7b6c05443a1b82fcca1525f9dc) ![{\displaystyle \operatorname {Cov} [X_{i},X_{j}]={\frac {\delta _{ij}\,{\tilde {\alpha }}_{i}-{\tilde {\alpha }}_{i}{\tilde {\alpha }}_{j}}{\alpha _{0}+1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5a10465175e4b932c563278e2f8b155dfd4fdbb)
where  , and , and  is the Kronecker delta is the Kronecker delta |
|---|
| Entropy |
  
with  defined as for variance, above; and defined as for variance, above; and  is the digamma function is the digamma function |
|---|
| Method of moments |
![{\displaystyle \alpha _{i}=E[X_{i}]\left({\frac {E[X_{j}](1-E[X_{j}])}{V[X_{j}]}}-1\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/027c83bab1eaa080e4ffb57d8a91db47f2a6c62f) where where  is any index, possibly is any index, possibly  itself itself |
|---|
In probability and statistics, the Dirichlet distribution (after Peter Gustav Lejeune Dirichlet), often denoted  , is a family of continuous multivariate probability distributions parameterized by a vector
, is a family of continuous multivariate probability distributions parameterized by a vector  of positive reals. It is a multivariate generalization of the beta distribution,[1] hence its alternative name of multivariate beta distribution (MBD).[2] Dirichlet distributions are commonly used as prior distributions in Bayesian statistics, and in fact, the Dirichlet distribution is the conjugate prior of the categorical distribution and multinomial distribution.
of positive reals. It is a multivariate generalization of the beta distribution,[1] hence its alternative name of multivariate beta distribution (MBD).[2] Dirichlet distributions are commonly used as prior distributions in Bayesian statistics, and in fact, the Dirichlet distribution is the conjugate prior of the categorical distribution and multinomial distribution.
The infinite-dimensional generalization of the Dirichlet distribution is the Dirichlet process.





![{\displaystyle x_{i}\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a32830173af0dc0eaf16f580cc75ef2f78b4f15e)




![{\displaystyle \operatorname {E} [X_{i}]={\frac {\alpha _{i}}{\alpha _{0}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dbec98ee7aeb59af97828e7b3e9fa92de937021d)
![{\displaystyle \operatorname {E} [\ln X_{i}]=\psi (\alpha _{i})-\psi (\alpha _{0})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a864ba2186ba3577dcd095b6b3f608511c668b53)


![{\displaystyle \operatorname {Var} [X_{i}]={\frac {{\tilde {\alpha }}_{i}(1-{\tilde {\alpha }}_{i})}{\alpha _{0}+1}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74281baf02f79a7b6c05443a1b82fcca1525f9dc)
![{\displaystyle \operatorname {Cov} [X_{i},X_{j}]={\frac {\delta _{ij}\,{\tilde {\alpha }}_{i}-{\tilde {\alpha }}_{i}{\tilde {\alpha }}_{j}}{\alpha _{0}+1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5a10465175e4b932c563278e2f8b155dfd4fdbb)






![{\displaystyle \alpha _{i}=E[X_{i}]\left({\frac {E[X_{j}](1-E[X_{j}])}{V[X_{j}]}}-1\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/027c83bab1eaa080e4ffb57d8a91db47f2a6c62f)



