| Disdyakis triacontahedron | |
|---|---|
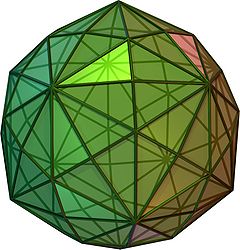 (rotating and 3D model) | |
| Type | Catalan |
| Conway notation | mD or dbD |
| Coxeter diagram | |
| Face polygon |  scalene triangle |
| Faces | 120 |
| Edges | 180 |
| Vertices | 62 = 12 + 20 + 30 |
| Face configuration | V4.6.10 |
| Symmetry group | Ih, H3, [5,3], (*532) |
| Rotation group | I, [5,3]+, (532) |
| Dihedral angle | |
| Dual polyhedron |  truncated icosidodecahedron |
| Properties | convex, face-transitive |
 net | |
In geometry, a disdyakis triacontahedron, hexakis icosahedron, decakis dodecahedron or kisrhombic triacontahedron[1] is a Catalan solid with 120 faces and the dual to the Archimedean truncated icosidodecahedron. As such it is face-uniform but with irregular face polygons. It slightly resembles an inflated rhombic triacontahedron: if one replaces each face of the rhombic triacontahedron with a single vertex and four triangles in a regular fashion, one ends up with a disdyakis triacontahedron. That is, the disdyakis triacontahedron is the Kleetope of the rhombic triacontahedron. It is also the barycentric subdivision of the regular dodecahedron and icosahedron. It has the most faces among the Archimedean and Catalan solids, with the snub dodecahedron, with 92 faces, in second place.
If the bipyramids, the gyroelongated bipyramids, and the trapezohedra are excluded, the disdyakis triacontahedron has the most faces of any other strictly convex polyhedron where every face of the polyhedron has the same shape.
Projected into a sphere, the edges of a disdyakis triacontahedron define 15 great circles. Buckminster Fuller used these 15 great circles, along with 10 and 6 others in two other polyhedra to define his 31 great circles of the spherical icosahedron.
- ^ Conway, Symmetries of things, p.284
