| Dodecadodecahedron | |
|---|---|
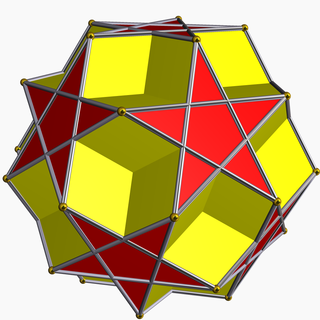
| |
| Type | Uniform star polyhedron |
| Elements | F = 24, E = 60 V = 30 (χ = −6) |
| Faces by sides | 12{5}+12{5/2} |
| Coxeter diagram | |
| Wythoff symbol | 2 | 5 5/2 2 | 5 5/3 2 | 5/2 5/4 2 | 5/3 5/4 |
| Symmetry group | Ih, [5,3], *532 |
| Index references | U36, C45, W73 |
| Dual polyhedron | Medial rhombic triacontahedron |
| Vertex figure |  5.5/2.5.5/2 |
| Bowers acronym | Did |

In geometry, the dodecadodecahedron is a nonconvex uniform polyhedron, indexed as U36.[1] It is the rectification of the great dodecahedron (and that of its dual, the small stellated dodecahedron). It was discovered independently by Hess (1878), Badoureau (1881) and Pitsch (1882).
The edges of this model form 10 central hexagons, and these, projected onto a sphere, become 10 great circles. These 10, along with the great circles from projections of two other polyhedra, form the 31 great circles of the spherical icosahedron used in construction of geodesic domes.
- ^ Maeder, Roman. "36: dodecadodecahedron". www.mathconsult.ch. Retrieved 2020-02-03.