Elongated triangular tiling

Elongated triangular tiling
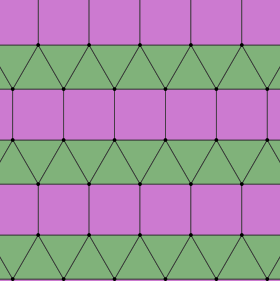Type	Semiregular tiling
Vertex configuration	3.3.3.4.4
Schläfli symbol	{3,6}:e s{∞}h1{∞}
Wythoff symbol	2 | 2 (2 2)
Coxeter diagram
Symmetry	cmm, [∞,2+,∞], (2*22)
Rotation symmetry	p2, [∞,2,∞]+, (2222)
Bowers acronym	Etrat
Dual	Prismatic pentagonal tiling
Properties	Vertex-transitive

In geometry, the elongated triangular tiling is a semiregular tiling of the Euclidean plane. There are three triangles and two squares on each vertex. It is named as a triangular tiling elongated by rows of squares, and given Schläfli symbol {3,6}:e.

Conway calls it a isosnub quadrille.^[1]

There are 3 regular and 8 semiregular tilings in the plane. This tiling is similar to the snub square tiling which also has 3 triangles and two squares on a vertex, but in a different order.