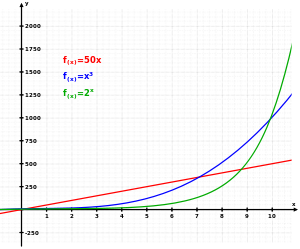
Exponential growth

Exponential growth occurs when a quantity grows at a rate directly proportional to its present size. For example, when it is 3 times as big as it is now, it will be growing 3 times as fast as it is now.

In more technical language, its instantaneous rate of change (that is, the derivative) of a quantity with respect to an independent variable is proportional to the quantity itself. Often the independent variable is time. Described as a function, a quantity undergoing exponential growth is an exponential function of time, that is, the variable representing time is the exponent (in contrast to other types of growth, such as quadratic growth). Exponential growth is the inverse of logarithmic growth.

Not all cases of growth at an always increasing rate are instances of exponential growth. For example the function ${\textstyle f(x)=x^{3}}$ grows at an ever increasing rate, but is very remote from growing exponentially. For example, when ${\textstyle x=1,}$ it grows at 3 times its size, but when ${\textstyle x=10}$ it grows at 30% of its size. If an exponentially growing function grows at a rate that is 3 times is present size, then it always grows at a rate that is 3 times its present size. When it is 10 times as big as it is now, it will grow 10 times as fast.

If the constant of proportionality is negative, then the quantity decreases over time, and is said to be undergoing exponential decay instead. In the case of a discrete domain of definition with equal intervals, it is also called geometric growth or geometric decay since the function values form a geometric progression.

The formula for exponential growth of a variable x at the growth rate r, as time t goes on in discrete intervals (that is, at integer times 0, 1, 2, 3, ...), is

$${\displaystyle x_{t}=x_{0}(1+r)^{t}}$$

where x₀ is the value of x at time 0. The growth of a bacterial colony is often used to illustrate it. One bacterium splits itself into two, each of which splits itself resulting in four, then eight, 16, 32, and so on. The amount of increase keeps increasing because it is proportional to the ever-increasing number of bacteria. Growth like this is observed in real-life activity or phenomena, such as the spread of virus infection, the growth of debt due to compound interest, and the spread of viral videos. In real cases, initial exponential growth often does not last forever, instead slowing down eventually due to upper limits caused by external factors and turning into logistic growth.

Terms like "exponential growth" are sometimes incorrectly interpreted as "rapid growth". Indeed, something that grows exponentially can in fact be growing slowly at first.^[1][2]