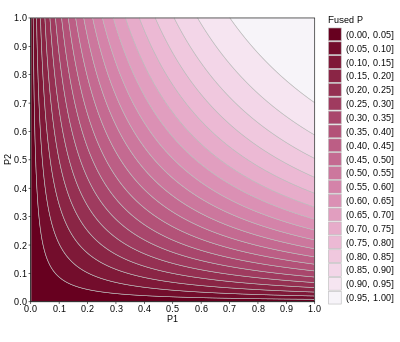
In statistics, Fisher's method,[1][2] also known as Fisher's combined probability test, is a technique for data fusion or "meta-analysis" (analysis of analyses). It was developed by and named for Ronald Fisher. In its basic form, it is used to combine the results from several independence tests bearing upon the same overall hypothesis (H0).
- ^ Fisher, R.A. (1925). Statistical Methods for Research Workers. Oliver and Boyd (Edinburgh). ISBN 0-05-002170-2.
- ^ Fisher, R.A.; Fisher, R. A (1948). "Questions and answers #14". The American Statistician. 2 (5): 30–31. doi:10.2307/2681650. JSTOR 2681650.