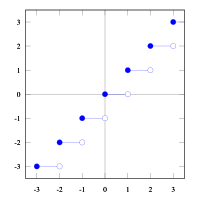
In mathematics, the floor function is the function that takes as input a real number x, and gives as output the greatest integer less than or equal to x, denoted ⌊x⌋ or floor(x). Similarly, the ceiling function maps x to the least integer greater than or equal to x, denoted ⌈x⌉ or ceil(x).[1]
For example, for floor: ⌊2.4⌋ = 2, ⌊−2.4⌋ = −3, and for ceiling: ⌈2.4⌉ = 3, and ⌈−2.4⌉ = −2.
The floor of x is also called the integral part, integer part, greatest integer, or entier of x, and was historically denoted [x] (among other notations).[2] However, the same term, integer part, is also used for truncation towards zero, which differs from the floor function for negative numbers.
For n an integer, ⌊n⌋ = ⌈n⌉ = n.
Although floor(x+1) and ceil(x) produce graphs that appear exactly alike, they are not the same when the value of x is an exact integer. For example, when x=2.0001; ⌊2.0001+1⌋ = ⌈2.0001⌉ = 3. However, if x=2, then ⌊2+1⌋ = 3, while ⌈2⌉ = 2.
| x | Floor ⌊x⌋ | Ceiling ⌈x⌉ | Fractional part {x} |
|---|---|---|---|
| 2 | 2 | 2 | 0 |
| 2.0001 | 2 | 3 | 0.0001 |
| 2.4 | 2 | 3 | 0.4 |
| 2.9 | 2 | 3 | 0.9 |
| 2.999 | 2 | 3 | 0.999 |
| −2.7 | −3 | −2 | 0.3 |
| −2 | −2 | −2 | 0 |
- ^ Graham, Knuth, & Patashnik, Ch. 3.1
- ^
1) Luke Heaton, A Brief History of Mathematical Thought, 2015, ISBN 1472117158 (n.p.)
2) Albert A. Blank et al., Calculus: Differential Calculus, 1968, p. 259
3) John W. Warris, Horst Stocker, Handbook of mathematics and computational science, 1998, ISBN 0387947469, p. 151