Flux balance analysis

This article may be too technical for most readers to understand. Please help improve it to make it understandable to non-experts, without removing the technical details. (February 2013) (Learn how and when to remove this message)

Flux balance analysis (FBA) is a mathematical method for simulating the metabolism of cells or entire unicellular organisms, such as E. coli or yeast, using genome-scale reconstructions of metabolic networks. Genome-scale reconstructions describe all the biochemical reactions in an organism based on its entire genome. These reconstructions model metabolism by focusing on the interactions between metabolites, identifying which metabolites are involved in the various reactions taking place in a cell or organism, and determining the genes that encode the enzymes catalyzing these reactions (if any). In comparison to traditional methods of modeling, FBA is less intensive in terms of the input data required for constructing the model. Simulations performed using FBA are computationally inexpensive and can calculate steady-state metabolic fluxes for large models (over 10,000 reactions) in a few seconds on modern personal computers. The related method of metabolic pathway analysis seeks to find and list all possible pathways between metabolites.

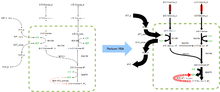
FBA finds applications in bioprocess engineering to systematically identify modifications to the metabolic networks of microbes used in fermentation processes that improve product yields of industrially important chemicals such as ethanol and succinic acid.^[2] It has also been used for the identification of putative drug targets in cancer ^[3] and pathogens,^[4] rational design of culture media,^[5] and host–pathogen interactions.^[6] The results of FBA can be visualized for smaller networks using flux maps similar to the image on the right, which illustrates the steady-state fluxes carried by reactions in glycolysis. The thickness of the arrows is proportional to the flux through the reaction.

FBA formalizes the system of equations describing the concentration changes in a metabolic network as the dot product of a matrix of the stoichiometric coefficients (the stoichiometric matrix S) and the vector v of the unsolved fluxes. The right-hand side of the dot product is a vector of zeros representing the system at steady state. At steady state, metabolite concentrations remain constant as the rates of production and consumption are balanced, resulting in no net change over time. Since the system of equations is often underdetermined, there can be multiple possible solutions. To obtain a single solution, the flux that maximizes a reaction of interest, such as biomass or ATP production, is selected. Linear programming is then used to calculate one of the possible solutions of fluxes corresponding to the steady state.