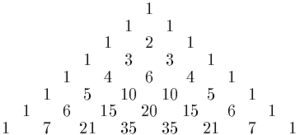
Gould's sequence

Pascal's triangle, rows 0 through 7. The number of odd integers in row i is the i-th number in Gould's sequence.
The self-similar sawtooth shape of Gould's sequence

Gould's sequence is an integer sequence named after Henry W. Gould that counts how many odd numbers are in each row of Pascal's triangle. It consists only of powers of two, and begins:[1][2]

1, 2, 2, 4, 2, 4, 4, 8, 2, 4, 4, 8, 4, 8, 8, 16, 2, 4, ... (sequence A001316 in the OEIS)

For instance, the sixth number in the sequence is 4, because there are four odd numbers in the sixth row of Pascal's triangle (the four bold numbers in the sequence 1, 5, 10, 10, 5, 1). Gould's sequence is also a fractal sequence.

  1. ^ Sloane, N. J. A. (ed.). "Sequence A001316 (Gould's sequence)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
  2. ^ Pólya, George; Tarjan, Robert E.; Woods, Donald R. (2009), Notes on Introductory Combinatorics, Progress in Computer Science and Applied Logic, vol. 4, Springer, p. 21, ISBN 9780817649531.