Graph isomorphism

In graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H

${\displaystyle f\colon V(G)\to V(H)}$

such that any two vertices u and v of G are adjacent in G if and only if ${\displaystyle f(u)}$ and ${\displaystyle f(v)}$ are adjacent in H. This kind of bijection is commonly described as "edge-preserving bijection", in accordance with the general notion of isomorphism being a structure-preserving bijection.

If an isomorphism exists between two graphs, then the graphs are called isomorphic and denoted as ${\displaystyle G\simeq H}$. In the case when the isomorphism is a mapping of a graph onto itself, i.e., when G and H are one and the same graph, the isomorphism is called an automorphism of G.

Graph isomorphism is an equivalence relation on graphs and as such it partitions the class of all graphs into equivalence classes. A set of graphs isomorphic to each other is called an isomorphism class of graphs. The question of whether graph isomorphism can be determined in polynomial time is a major unsolved problem in computer science, known as the graph isomorphism problem.^[1][2]

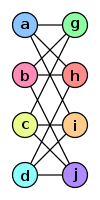
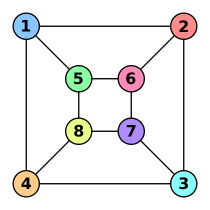
The two graphs shown below are isomorphic, despite their different looking drawings.

Graph G	Graph H	An isomorphism between G and H
		f(a) = 1 f(b) = 6 f(c) = 8 f(d) = 3 f(g) = 5 f(h) = 2 f(i) = 4 f(j) = 7