Halved cube graph

Halved cube graph
The halved cube graph ⁠1/2⁠Q3
Vertices2n–1
Edgesn(n – 1)2n–3
Automorphismsn! 2n–1, for n > 4
n! 2n, for n = 4
(2n–1)!, for n < 4[1]
PropertiesSymmetric
Distance regular
Notation⁠1/2⁠Qn
Table of graphs and parameters
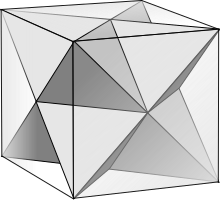
Construction of two demicubes (regular tetrahedra, forming a stella octangula) from a single cube. The halved cube graph of dimension three is the graph of vertices and edges of a single demicube. The halved cube graph of dimension four includes all of the cube vertices and edges, and all of the edges of the two demicubes.

In graph theory, the halved cube graph or half cube graph of dimension n is the graph of the demihypercube, formed by connecting pairs of vertices at distance exactly two from each other in the hypercube graph. That is, it is the half-square of the hypercube. This connectivity pattern produces two isomorphic graphs, disconnected from each other, each of which is the halved cube graph.

  1. ^ A.E. Brouwer, A.M. Cohen, and A. Neumaier (1989), Distance Regular Graphs. Berlin, New York: Springer-Verlag, p. 265. ISBN 3-540-50619-5, ISBN 0-387-50619-5