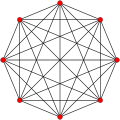
 7-simplex |
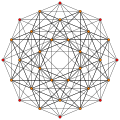 Hexicated 7-simplex |
 Hexitruncated 7-simplex |
 Hexicantellated 7-simplex |
 Hexiruncinated 7-simplex |
 Hexicantitruncated 7-simplex |
 Hexiruncitruncated 7-simplex |
 Hexiruncicantellated 7-simplex |
 Hexisteritruncated 7-simplex |
 Hexistericantellated 7-simplex |
 Hexipentitruncated 7-simplex |
 Hexiruncicantitruncated 7-simplex |
 Hexistericantitruncated 7-simplex |
 Hexisteriruncitruncated 7-simplex |
 Hexisteriruncicantellated 7-simplex |
 Hexipenticantitruncated 7-simplex |
 Hexipentiruncitruncated 7-simplex |
 Hexisteriruncicantitruncated 7-simplex |
 Hexipentiruncicantitruncated 7-simplex |
 Hexipentistericantitruncated 7-simplex |
 Hexipentisteriruncicantitruncated 7-simplex (Omnitruncated 7-simplex) | |||
| Orthogonal projections in A7 Coxeter plane | |||
|---|---|---|---|
In seven-dimensional geometry, a hexicated 7-simplex is a convex uniform 7-polytope, including 6th-order truncations (hexication) from the regular 7-simplex.
There are 20 unique hexications for the 7-simplex, including all permutations of truncations, cantellations, runcinations, sterications, and pentellations.
The simple hexicated 7-simplex is also called an expanded 7-simplex, with only the first and last nodes ringed, is constructed by an expansion operation applied to the regular 7-simplex. The highest form, the hexipentisteriruncicantitruncated 7-simplex is more simply called a omnitruncated 7-simplex with all of the nodes ringed.