Hill sphere

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages) This scientific article needs additional citations to secondary or tertiary sources. Help add sources such as review articles, monographs, or textbooks. Please also establish the relevance for any primary research articles cited. Unsourced or poorly sourced material may be challenged and removed. (July 2023) (Learn how and when to remove this message) The article's lead section may need to be rewritten. Relevant discussion may be found on Talk:Hill sphere. Please help improve the lead and read the lead layout guide. (April 2024) (Learn how and when to remove this message) (Learn how and when to remove this message)

Part of a series on
Astrodynamics
Orbital mechanics
Orbital elements Apsis Argument of periapsis Eccentricity Inclination Mean anomaly Orbital nodes Semi-major axis True anomaly
Types of two-body orbits by eccentricity Circular orbit Elliptic orbit Transfer orbit (Hohmann transfer orbit Bi-elliptic transfer orbit) Parabolic orbit Hyperbolic orbit Radial orbit Decaying orbit
Equations Dynamical friction Escape velocity Kepler's equation Kepler's laws of planetary motion Orbital period Orbital velocity Surface gravity Specific orbital energy Vis-viva equation
Celestial mechanics
Gravitational influences Barycenter Hill sphere Perturbations Sphere of influence
N-body orbits Lagrangian points (Halo orbits) Lissajous orbits Lyapunov orbits
Engineering and efficiency
Preflight engineering Mass ratio Payload fraction Propellant mass fraction Tsiolkovsky rocket equation
Efficiency measures Gravity assist Oberth effect
Propulsive maneuvers Orbital maneuver Orbit insertion
v t e

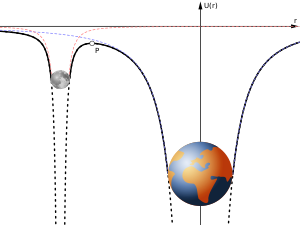
The Hill sphere is a common model for the calculation of a gravitational sphere of influence. It is the most commonly used model to calculate the spatial extent of gravitational influence of an astronomical body (m) in which it dominates over the gravitational influence of other bodies, particularly a primary (M).^[1] It is sometimes confused with other models of gravitational influence, such as the Laplace sphere^[1] or being named the Roche sphere, the latter causing confusion with the Roche limit.^[2][3] It was defined by the American astronomer George William Hill, based on the work of the French astronomer Édouard Roche.^{[not verified in body]}

To be retained by a more gravitationally attracting astrophysical object—a planet by a more massive star, a moon by a more massive planet—the less massive body must have an orbit that lies within the gravitational potential represented by the more massive body's Hill sphere.^{[not verified in body]} That moon would, in turn, have a Hill sphere of its own, and any object within that distance would tend to become a satellite of the moon, rather than of the planet itself.^{[not verified in body]}

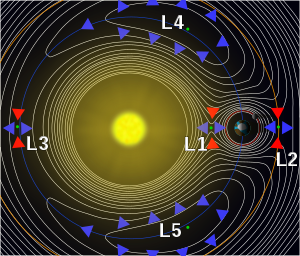
One simple view of the extent of the Solar System is that it is bounded by the Hill sphere of the Sun (engendered by the Sun's interaction with the galactic nucleus or other more massive stars).^{[4][verification needed]} A more complex example is the one at right, the Earth's Hill sphere, which extends between the Lagrange points L₁ and L₂,^{[clarification needed]} which lie along the line of centers of the Earth and the more massive Sun.^{[not verified in body]} The gravitational influence of the less massive body is least in that direction, and so it acts as the limiting factor for the size of the Hill sphere;^{[clarification needed]} beyond that distance, a third object in orbit around the Earth would spend at least part of its orbit outside the Hill sphere, and would be progressively perturbed by the tidal forces of the more massive body, the Sun, eventually ending up orbiting the latter.^{[not verified in body]}

For two massive bodies with gravitational potentials and any given energy of a third object of negligible mass interacting with them, one can define a zero-velocity surface in space which cannot be passed, the contour of the Jacobi integral.^{[not verified in body]} When the object's energy is low, the zero-velocity surface completely surrounds the less massive body (of this restricted three-body system), which means the third object cannot escape; at higher energy, there will be one or more gaps or bottlenecks by which the third object may escape the less massive body and go into orbit around the more massive one.^{[not verified in body]} If the energy is at the border between these two cases, then the third object cannot escape, but the zero-velocity surface confining it touches a larger zero-velocity surface around the less massive body^{[verification needed]} at one of the nearby Lagrange points, forming a cone-like point there.^{[clarification needed][not verified in body]} At the opposite side of the less massive body, the zero-velocity surface gets close to the other Lagrange point.^{[not verified in body]}