| Set of regular n-gonal hosohedra | |
|---|---|
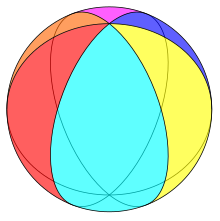 Example regular hexagonal hosohedron on a sphere | |
| Type | regular polyhedron or spherical tiling |
| Faces | n digons |
| Edges | n |
| Vertices | 2 |
| Euler char. | 2 |
| Vertex configuration | 2n |
| Wythoff symbol | n | 2 2 |
| Schläfli symbol | {2,n} |
| Coxeter diagram | |
| Symmetry group | Dnh [2,n] (*22n) order 4n |
| Rotation group | Dn [2,n]+ (22n) order 2n |
| Dual polyhedron | regular n-gonal dihedron |

In spherical geometry, an n-gonal hosohedron is a tessellation of lunes on a spherical surface, such that each lune shares the same two polar opposite vertices.
A regular n-gonal hosohedron has Schläfli symbol {2,n}, with each spherical lune having internal angle 2π/nradians (360/n degrees).[1][2]