|
Probability density function 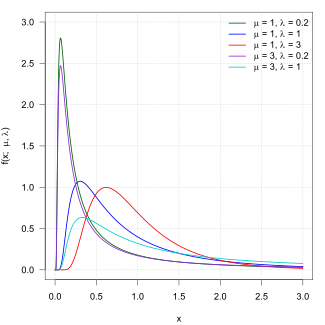 | |||
|
Cumulative distribution function 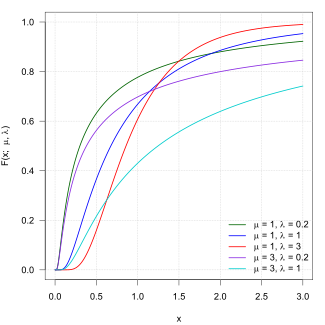 | |||
| Notation | |||
|---|---|---|---|
| Parameters |
| ||
| Support | |||
| CDF |
where is the standard normal (standard Gaussian) distribution c.d.f. | ||
| Mean |
| ||
| Mode | |||
| Variance |
| ||
| Skewness | |||
| Excess kurtosis | |||
| MGF | |||
| CF | |||
In probability theory, the inverse Gaussian distribution (also known as the Wald distribution) is a two-parameter family of continuous probability distributions with support on (0,∞).
Its probability density function is given by
for x > 0, where is the mean and is the shape parameter.[1]
The inverse Gaussian distribution has several properties analogous to a Gaussian distribution. The name can be misleading: it is an "inverse" only in that, while the Gaussian describes a Brownian motion's level at a fixed time, the inverse Gaussian describes the distribution of the time a Brownian motion with positive drift takes to reach a fixed positive level.
Its cumulant generating function (logarithm of the characteristic function)[contradictory] is the inverse of the cumulant generating function of a Gaussian random variable.
To indicate that a random variable X is inverse Gaussian-distributed with mean μ and shape parameter λ we write .




![{\displaystyle {\sqrt {\frac {\lambda }{2\pi x^{3}}}}\exp \left[-{\frac {\lambda (x-\mu )^{2}}{2\mu ^{2}x}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1aa826bd14dafa233ecf825205556f3fd63f4036)



![{\displaystyle \operatorname {E} [X]=\mu }](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e19f2ee2d8e606b7b96a6667b3e8cd403851b53)
![{\displaystyle \operatorname {E} [{\frac {1}{X}}]={\frac {1}{\mu }}+{\frac {1}{\lambda }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e36ffbc215910090ddcde7459852222b5fefc46)
![{\displaystyle \mu \left[\left(1+{\frac {9\mu ^{2}}{4\lambda ^{2}}}\right)^{\frac {1}{2}}-{\frac {3\mu }{2\lambda }}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/faccc6b138a2e92276195b63131d43ff17aca2c3)
![{\displaystyle \operatorname {Var} [X]={\frac {\mu ^{3}}{\lambda }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ef3cb89b672f779526e832cc744119392bd3a7c)
![{\displaystyle \operatorname {Var} [{\frac {1}{X}}]={\frac {1}{\mu \lambda }}+{\frac {2}{\lambda ^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/96cc7549c1f05926a4ab710648ea7171149ae760)


![{\displaystyle \exp \left[{{\frac {\lambda }{\mu }}\left(1-{\sqrt {1-{\frac {2\mu ^{2}t}{\lambda }}}}\right)}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85fd70a416cd4eca18b79cc2056182488e50b6e4)
![{\displaystyle \exp \left[{{\frac {\lambda }{\mu }}\left(1-{\sqrt {1-{\frac {2\mu ^{2}\mathrm {i} t}{\lambda }}}}\right)}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74fb6c22f7b30c53d82f1d548fa13fc4384e4749)

