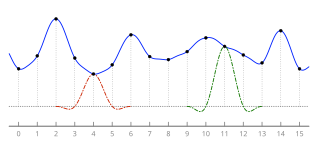
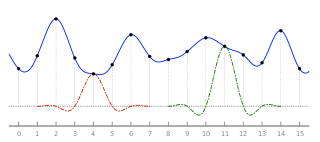
Lanczos filtering and Lanczos resampling are two applications of a certain mathematical formula. It can be used as a low-pass filter or used to smoothly interpolate the value of a digital signal between its samples. In the latter case, it maps each sample of the given signal to a translated and scaled copy of the Lanczos kernel, which is a sinc function windowed by the central lobe of a second, longer, sinc function. The sum of these translated and scaled kernels is then evaluated at the desired points.
Lanczos resampling is typically used to increase the sampling rate of a digital signal, or to shift it by a fraction of the sampling interval. It is often used also for multivariate interpolation, for example to resize or rotate a digital image. It has been considered the "best compromise" among several simple filters for this purpose.[1]
The filter was invented by Claude Duchon, who named it after Cornelius Lanczos due to Duchon's use of Sigma approximation in constructing the filter, a technique created by Lanczos.[2]
- ^ Turkowski, Ken; Gabriel, Steve (1990). "Filters for Common Resampling Tasks". In Glassner, Andrew S. (ed.). Graphics Gems I. Academic Press. pp. 147–165. CiteSeerX 10.1.1.116.7898. ISBN 978-0-12-286165-9.
- ^ Claude, Duchon (1979-08-01). "Lanczos Filtering in One and Two Dimensions". Journal of Applied Meteorology. 18 (8): 1016–1022. Bibcode:1979JApMe..18.1016D. doi:10.1175/1520-0450(1979)018<1016:LFIOAT>2.0.CO;2.