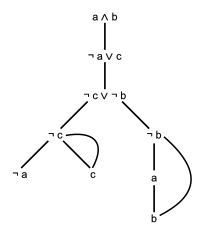
In proof theory, the semantic tableau[1] (/tæˈbloʊ, ˈtæbloʊ/; plural: tableaux), also called an analytic tableau,[2] truth tree,[1] or simply tree,[2] is a decision procedure for sentential and related logics, and a proof procedure for formulae of first-order logic.[1] An analytic tableau is a tree structure computed for a logical formula, having at each node a subformula of the original formula to be proved or refuted. Computation constructs this tree and uses it to prove or refute the whole formula.[3] The tableau method can also determine the satisfiability of finite sets of formulas of various logics. It is the most popular proof procedure for modal logics.[4]
A method of truth trees contains a fixed set of rules for producing trees from a given logical formula, or set of logical formulas. Those trees will have more formulas at each branch, and in some cases, a branch can come to contain both a formula and its negation, which is to say, a contradiction. In that case, the branch is said to close.[1] If every branch in a tree closes, the tree itself is said to close. In virtue of the rules for construction of tableaux, a closed tree is a proof that the original formula, or set of formulas, used to construct it was itself self-contradictory,[1] and therefore false. Conversely, a tableau can also prove that a logical formula is tautologous: if a formula is tautologous, its negation is a contradiction, so a tableau built from its negation will close.[1]
- ^ a b c d e f Howson, Colin (1997). Logic with trees: an introduction to symbolic logic. London; New York: Routledge. pp. ix, x, 24–29, 47. ISBN 978-0-415-13342-5.
- ^ a b Restall, Greg (2006). Logic: an introduction. Fundamentals of philosophy. London; New York: Routledge. pp. 5, 42, 55. ISBN 978-0-415-40067-1. OCLC 63115330.
- ^ Howson 2005, p. 27.
- ^ Girle 2014.