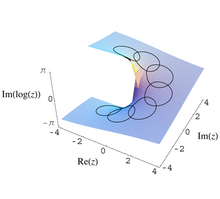
In mathematics, monodromy is the study of how objects from mathematical analysis, algebraic topology, algebraic geometry and differential geometry behave as they "run round" a singularity. As the name implies, the fundamental meaning of monodromy comes from "running round singly". It is closely associated with covering maps and their degeneration into ramification; the aspect giving rise to monodromy phenomena is that certain functions we may wish to define fail to be single-valued as we "run round" a path encircling a singularity. The failure of monodromy can be measured by defining a monodromy group: a group of transformations acting on the data that encodes what happens as we "run round" in one dimension. Lack of monodromy is sometimes called polydromy.[1]
- ^ König, Wolfgang; Sprekels, Jürgen (2015). Karl Weierstraß (1815–1897): Aspekte seines Lebens und Werkes – Aspects of his Life and Work (in German). Springer-Verlag. pp. 200–201. ISBN 9783658106195. Retrieved 5 October 2017.