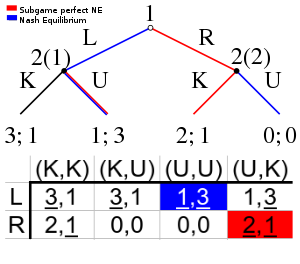
A non-credible threat is a term used in game theory and economics to describe a threat in a sequential game that a rational player would not actually carry out, because it would not be in his best interest to do so.
A threat, and its counterpart – a commitment, are both defined by American economist and Nobel prize winner, T.C. Schelling, who stated that: "A announces that B's behaviour will lead to a response from A. If this response is a reward, then the announcement is a commitment; if this response is a penalty, then the announcement is a threat."[1] While a player might make a threat, it is only deemed credible if it serves the best interest of the player.[2] In other words, the player would be willing to carry through with the action that is being threatened regardless of the choice of the other player.[3] This is based on the assumption that the player is rational.[1]
A non-credible threat is made on the hope that it will be believed, and therefore the threatening undesirable action will not need to be carried out.[4] For a threat to be credible within an equilibrium, whenever a node is reached where a threat should be fulfilled, it will be fulfilled.[3] Those Nash equilibria that rely on non-credible threats can be eliminated through backward induction; the remaining equilibria are called subgame perfect Nash equilibria.[2][5]
- ^ a b Sun, Shaorong; Sun, Na (2018). Management Game Theory. doi:10.1007/978-981-13-1062-1. ISBN 978-981-13-1061-4. S2CID 169075970.
- ^ a b Heifetz, A., & Yalon-Fortus, J. (2012). Game Theory: Interactive Strategies in Economics and Management. Cambridge University Press. ProQuest Ebook Central
- ^ a b Schelling, Thomas C. (1956). "An Essay on Bargaining". The American Economic Review. 46 (3): 281–306. JSTOR 1805498.
- ^ Cite error: The named reference
VanDammewas invoked but never defined (see the help page). - ^ Harrington, J. E. (1989). "Noncooperative Games". In Eatwell, John; Milgate, Murray; Newman, Peter (eds.). Game Theory. Palgrave Macmillan. pp. 178–184. doi:10.1007/978-1-349-20181-5. ISBN 978-1-349-20181-5.