Parallel curve

Not to be confused with parallel transport.
Parallel curves of the graph of for distances
Two definitions of a parallel curve: 1) envelope of a family of congruent circles, 2) by a fixed normal distance
The parallel curves of a circle (red) are circles, too

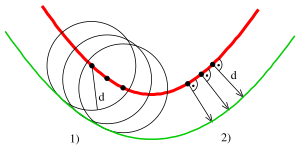
A parallel of a curve is the envelope of a family of congruent circles centered on the curve. It generalises the concept of parallel (straight) lines. It can also be defined as a curve whose points are at a constant normal distance from a given curve.[1] These two definitions are not entirely equivalent as the latter assumes smoothness, whereas the former does not.[2]

In computer-aided design the preferred term for a parallel curve is offset curve.[2][3][4] (In other geometric contexts, the term offset can also refer to translation.[5]) Offset curves are important, for example, in numerically controlled machining, where they describe, for example, the shape of the cut made by a round cutting tool of a two-axis machine. The shape of the cut is offset from the trajectory of the cutter by a constant distance in the direction normal to the cutter trajectory at every point.[6]

In the area of 2D computer graphics known as vector graphics, the (approximate) computation of parallel curves is involved in one of the fundamental drawing operations, called stroking, which is typically applied to polylines or polybeziers (themselves called paths) in that field.[7]

Except in the case of a line or circle, the parallel curves have a more complicated mathematical structure than the progenitor curve.[1] For example, even if the progenitor curve is smooth, its offsets may not be so; this property is illustrated in the top figure, using a sine curve as progenitor curve.[2] In general, even if a curve is rational, its offsets may not be so. For example, the offsets of a parabola are rational curves, but the offsets of an ellipse or of a hyperbola are not rational, even though these progenitor curves themselves are rational.[3]

The notion also generalizes to 3D surfaces, where it is called an offset surface or parallel surface.[8] Increasing a solid volume by a (constant) distance offset is sometimes called dilation.[9] The opposite operation is sometimes called shelling.[8] Offset surfaces are important in numerically controlled machining, where they describe the shape of the cut made by a ball nose end mill of a three-axis machine.[10] Other shapes of cutting bits can be modelled mathematically by general offset surfaces.[11]

  1. ^ a b Willson, Frederick Newton (1898). Theoretical and Practical Graphics. Macmillan. p. 66. ISBN 978-1-113-74312-1.
  2. ^ a b c Devadoss, Satyan L.; O'Rourke, Joseph (2011). Discrete and Computational Geometry. Princeton University Press. pp. 128–129. ISBN 978-1-4008-3898-1.
  3. ^ a b Sendra, J. Rafael; Winkler, Franz; Pérez Díaz, Sonia (2007). Rational Algebraic Curves: A Computer Algebra Approach. Springer Science & Business Media. p. 10. ISBN 978-3-540-73724-7.
  4. ^ Agoston, Max K. (2005). Computer Graphics and Geometric Modelling: Mathematics. Springer Science & Business Media. p. 586. ISBN 978-1-85233-817-6.
  5. ^ Vince, John (2006). Geometry for Computer Graphics: Formulae, Examples and Proofs. Springer Science & Business Media. p. 293. ISBN 978-1-84628-116-7.
  6. ^ Marsh, Duncan (2006). Applied Geometry for Computer Graphics and CAD (2nd ed.). Springer Science & Business Media. p. 107. ISBN 978-1-84628-109-9.
  7. ^ Mark Kilgard (2012-04-10). "CS 354 Vector Graphics & Path Rendering". www.slideshare.net. p. 28.
  8. ^ a b Agoston, Max K. (2005). Computer Graphics and Geometric Modelling. Springer Science & Business Media. pp. 638–645. ISBN 978-1-85233-818-3.
  9. ^ http://www.cc.gatech.edu/~jarek/papers/localVolume.pdf, p. 3
  10. ^ Faux, I. D.; Pratt, Michael J. (1979). Computational Geometry for Design and Manufacture. Halsted Press. ISBN 978-0-47026-473-7. OCLC 4859052.
  11. ^ Brechner, Eric (1990). Envelopes and tool paths for three-axis end milling (PhD). Rensselaer Polytechnic Institute.