| Condensed matter physics |
|---|
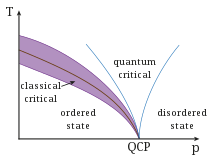 |

A polymer is a macromolecule, composed of many similar or identical repeated subunits. Polymers are common in, but not limited to, organic media. They range from familiar synthetic plastics to natural biopolymers such as DNA and proteins. Their unique elongated molecular structure produces unique physical properties, including toughness, viscoelasticity, and a tendency to form glasses and semicrystalline structures. The modern concept of polymers as covalently bonded macromolecular structures was proposed in 1920 by Hermann Staudinger.[1] One sub-field in the study of polymers is polymer physics. As a part of soft matter studies, Polymer physics concerns itself with the study of mechanical properties[2] and focuses on the perspective of condensed matter physics.
Because polymers are such large molecules, bordering on the macroscopic scale, their physical properties are usually too complicated for solving using deterministic methods. Therefore, statistical approaches are often implemented to yield pertinent results. The main reason for this relative success is that polymers constructed from a large number of monomers are efficiently described in the thermodynamic limit of infinitely many monomers, although in actuality they are obviously finite in size.
Thermal fluctuations continuously affect the shape of polymers in liquid solutions, and modeling their effect requires using principles from statistical mechanics and dynamics. The path integral approach falls in line with this basic premise and its afforded results are unvaryingly statistical averages. The path integral, when applied to the study of polymers, is essentially a mathematical mechanism to describe, count and statistically weigh all possible spatial configuration a polymer can conform to under well defined potential and temperature circumstances. Employing path integrals, problems hitherto unsolved were successfully worked out: Excluded volume, entanglement, links and knots to name a few.[3] Prominent contributors to the development of the theory include Nobel laureate P.G. de Gennes, Sir Sam Edwards, M.Doi,[4][5] F.W. Wiegel[3] and H. Kleinert.[6]
- ^ H.R Allcock; F.W. Lampe; J.E Mark, Contemporary Polymer Chemistry (3 ed.). (Pearson Education 2003). p. 21. ISBN 0-13-065056-0.
- ^ P. Flory, Principles of Polymer Chemistry, Cornell University Press, 1953. ISBN 0-8014-0134-8.
- ^ a b F.W. Wiegel, Introduction to Path-Integral Methods in Physics and Polymer science (World Scientific, Philadelphia, 1986).
- ^ Doi, Masao; Edwards, S. F. (1978). "Dynamics of concentrated polymer systems. Part 1—3". J. Chem. Soc., Faraday Trans. 2. 74. Royal Society of Chemistry (RSC): 1789–1832. doi:10.1039/f29787401789. ISSN 0300-9238.
- ^ Doi, Masao; Edwards, S. F. (1979). "Dynamics of concentrated polymer systems. Part 4.—Rheological properties". J. Chem. Soc., Faraday Trans. 2. 75. Royal Society of Chemistry (RSC): 38–54. doi:10.1039/f29797500038. ISSN 0300-9238.
- ^ H. Kleinert, PATH INTEGRALS in Quantum mechanics, Statistics, Polymer Physics, and Financial Markets (World Scientific, 2009).