| Pentakis dodecahedron | |
|---|---|
 (Click here for rotating model) | |
| Type | Catalan solid |
| Coxeter diagram | |
| Conway notation | kD |
| Face type | V5.6.6 isosceles triangle |
| Faces | 60 |
| Edges | 90 |
| Vertices | 32 |
| Vertices by type | 20{6}+12{5} |
| Symmetry group | Ih, H3, [5,3], (*532) |
| Rotation group | I, [5,3]+, (532) |
| Dihedral angle | 156°43′07″ arccos(−80 + 9√5/109) |
| Properties | convex, face-transitive |
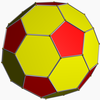 Truncated icosahedron (dual polyhedron) |
 Net |

In geometry, a pentakis dodecahedron or kisdodecahedron is a polyhedron created by attaching a pentagonal pyramid to each face of a regular dodecahedron; that is, it is the Kleetope of the dodecahedron. Specifically, the term typically refers to a particular Catalan solid, namely the dual of a truncated icosahedron.