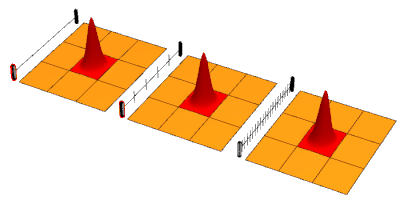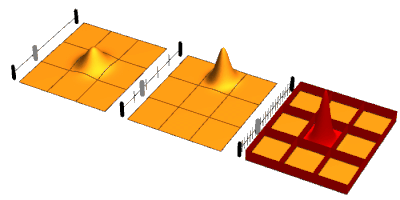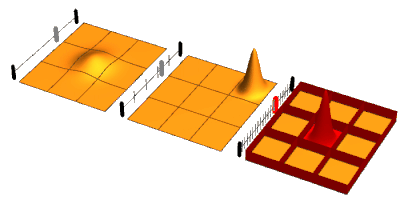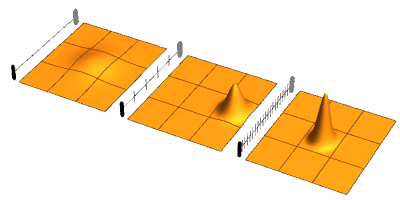
The quantum Zeno effect (also known as the Turing paradox) is a feature of quantum-mechanical systems allowing a particle's time evolution to be slowed down by measuring it frequently enough with respect to some chosen measurement setting.[1]
Sometimes this effect is interpreted as "a system cannot change while you are watching it".[2] One can "freeze" the evolution of the system by measuring it frequently enough in its known initial state. The meaning of the term has since expanded, leading to a more technical definition, in which time evolution can be suppressed not only by measurement: the quantum Zeno effect is the suppression of unitary time evolution in quantum systems provided by a variety of sources: measurement, interactions with the environment, stochastic fields, among other factors.[3] As an outgrowth of study of the quantum Zeno effect, it has become clear that applying a series of sufficiently strong and fast pulses with appropriate symmetry can also decouple a system from its decohering environment.[4]
The first rigorous and general derivation of the quantum Zeno effect was presented in 1974 by Antonio Degasperis, Luciano Fonda, and Giancarlo Ghirardi,[5] although it had previously been described by Alan Turing.[6] The comparison with Zeno's paradox is due to a 1977 article by Baidyanath Misra & E. C. George Sudarshan. The name comes by analogy to Zeno's arrow paradox, which states that because an arrow in flight is not seen to move during any single instant, it cannot possibly be moving at all. In the quantum Zeno effect an unstable state seems frozen – to not 'move' – due to a constant series of observations.
According to the reduction postulate, each measurement causes the wavefunction to collapse to an eigenstate of the measurement basis. In the context of this effect, an observation can simply be the absorption of a particle, without the need of an observer in any conventional sense. However, there is controversy over the interpretation of the effect, sometimes referred to as the "measurement problem" in traversing the interface between microscopic and macroscopic objects.[7][8]
Another crucial problem related to the effect is strictly connected to the time–energy indeterminacy relation (part of the indeterminacy principle). If one wants to make the measurement process more and more frequent, one has to correspondingly decrease the time duration of the measurement itself. But the request that the measurement last only a very short time implies that the energy spread of the state in which reduction occurs becomes increasingly large. However, the deviations from the exponential decay law for small times is crucially related to the inverse of the energy spread, so that the region in which the deviations are appreciable shrinks when one makes the measurement process duration shorter and shorter. An explicit evaluation of these two competing requests shows that it is inappropriate, without taking into account this basic fact, to deal with the actual occurrence and emergence of Zeno's effect.[9]
Closely related (and sometimes not distinguished from the quantum Zeno effect) is the watchdog effect, in which the time evolution of a system is affected by its continuous coupling to the environment.[10][11][12][13]
- ^ Sudarshan, E. C. G.; Misra, B. (1977). "The Zeno's paradox in quantum theory". Journal of Mathematical Physics. 18 (4): 756–763. Bibcode:1977JMP....18..756M. doi:10.1063/1.523304. OSTI 7342282.
- ^ https://phys.org/news/2015-10-zeno-effect-verifiedatoms-wont.html. Archived 2018-09-25 at the Wayback Machine
- ^ Nakanishi, T.; Yamane, K.; Kitano, M. (2001). "Absorption-free optical control of spin systems: the quantum Zeno effect in optical pumping". Physical Review A. 65 (1): 013404. arXiv:quant-ph/0103034. Bibcode:2001PhRvA..65a3404N. doi:10.1103/PhysRevA.65.013404. S2CID 56052019.
- ^ Facchi, P.; Lidar, D. A.; Pascazio, S. (2004). "Unification of dynamical decoupling and the quantum Zeno effect". Physical Review A. 69 (3): 032314. arXiv:quant-ph/0303132. Bibcode:2004PhRvA..69c2314F. doi:10.1103/PhysRevA.69.032314. S2CID 38253718.
- ^ Degasperis, A.; Fonda, L.; Ghirardi, G. C. (1974). "Does the lifetime of an unstable system depend on the measuring apparatus?". Il Nuovo Cimento A. 21 (3): 471–484. Bibcode:1974NCimA..21..471D. doi:10.1007/BF02731351. S2CID 120279111.
- ^ Hofstadter, D. (2004). Teuscher, C. (ed.). Alan Turing: Life and Legacy of a Great Thinker. Springer. p. 54. ISBN 978-3-540-20020-8.
- ^ Greenstein, G.; Zajonc, A. (2005). The Quantum Challenge: Modern Research on the Foundations of Quantum Mechanics. Jones & Bartlett Publishers. p. 237. ISBN 978-0-7637-2470-2.
- ^ Facchi, P.; Pascazio, S. (2002). "Quantum Zeno subspaces". Physical Review Letters. 89 (8): 080401. arXiv:quant-ph/0201115. Bibcode:2002PhRvL..89h0401F. doi:10.1103/PhysRevLett.89.080401. PMID 12190448. S2CID 29178016.
- ^ Ghirardi, G. C.; Omero, C.; Rimini, A.; Weber, T. (1979). "Small Time Behaviour of Quantum Nondecay Probability and Zeno's Paradox in Quantum Mechanics". Il Nuovo Cimento A. 52 (4): 421. Bibcode:1979NCimA..52..421G. doi:10.1007/BF02770851. S2CID 124911216.
- ^ Kraus, K. (1981-08-01). "Measuring processes in quantum mechanics I. Continuous observation and the watchdog effect". Foundations of Physics. 11 (7–8): 547–576. Bibcode:1981FoPh...11..547K. doi:10.1007/bf00726936. ISSN 0015-9018. S2CID 121902392.
- ^ Belavkin, V.; Staszewski, P. (1992). "Nondemolition observation of a free quantum particle". Phys. Rev. A. 45 (3): 1347–1356. arXiv:quant-ph/0512138. Bibcode:1992PhRvA..45.1347B. doi:10.1103/PhysRevA.45.1347. PMID 9907114. S2CID 14637898.
- ^ Ghose, P. (1999). Testing Quantum Mechanics on New Ground. Cambridge University Press. p. 114. ISBN 978-0-521-02659-8.
- ^ Auletta, G. (2000). Foundations and Interpretation of Quantum Mechanics. World Scientific. p. 341. ISBN 978-981-02-4614-3.