Quarter cubic honeycomb

Quarter cubic honeycomb
Type	Uniform honeycomb
Family	Truncated simplectic honeycomb Quarter hypercubic honeycomb
Indexing[1]	J25,33, A13 W10, G6
Schläfli symbol	t0,1{3[4]} or q{4,3,4}
Coxeter-Dynkin diagram	= =
Cell types	{3,3} (3.6.6)
Face types	{3}, {6}
Vertex figure	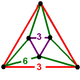(isosceles triangular antiprism)
Space group	Fd3m (227)
Coxeter group	${\displaystyle {\tilde {A}}_{3}}$×22, [[3[4]]]
Dual	oblate cubille Cell: (1/4 of rhombic dodecahedron)
Properties	vertex-transitive, edge-transitive

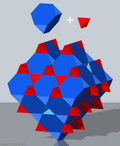
The quarter cubic honeycomb, quarter cubic cellulation or bitruncated alternated cubic honeycomb is a space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of tetrahedra and truncated tetrahedra in a ratio of 1:1. It is called "quarter-cubic" because its symmetry unit – the minimal block from which the pattern is developed by reflections – is four times that of the cubic honeycomb.

It is vertex-transitive with 6 truncated tetrahedra and 2 tetrahedra around each vertex.

A geometric honeycomb is a space-filling of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions.

Honeycombs are usually constructed in ordinary Euclidean ("flat") space, like the convex uniform honeycombs. They may also be constructed in non-Euclidean spaces, such as hyperbolic uniform honeycombs. Any finite uniform polytope can be projected to its circumsphere to form a uniform honeycomb in spherical space.

It is one of the 28 convex uniform honeycombs.

The faces of this honeycomb's cells form four families of parallel planes, each with a 3.6.3.6 tiling.

Its vertex figure is an isosceles antiprism: two equilateral triangles joined by six isosceles triangles.

John Horton Conway calls this honeycomb a truncated tetrahedrille, and its dual oblate cubille.

The vertices and edges represent a Kagome lattice in three dimensions,^[2] which is the pyrochlore lattice.