Quarter hypercubic honeycomb

In geometry, the quarter hypercubic honeycomb (or quarter n-cubic honeycomb) is a dimensional infinite series of honeycombs, based on the hypercube honeycomb. It is given a Schläfli symbol q{4,3...3,4} or Coxeter symbol qδ₄ representing the regular form with three quarters of the vertices removed and containing the symmetry of Coxeter group ${\displaystyle {\tilde {D}}_{n-1}}$ for n ≥ 5, with ${\displaystyle {\tilde {D}}_{4}}$ = ${\displaystyle {\tilde {A}}_{4}}$ and for quarter n-cubic honeycombs ${\displaystyle {\tilde {D}}_{5}}$ = ${\displaystyle {\tilde {B}}_{5}}$.^[1]

qδn	Name	Schläfli symbol	Coxeter diagrams	Facets			Vertex figure
qδ3	quarter square tiling	q{4,4}	or or	h{4}={2}	{ }×{ }		{ }×{ }
qδ4	quarter cubic honeycomb	q{4,3,4}	or o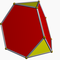r	h{4,3}	h2{4,3}		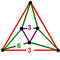Elongated triangular antiprism
qδ5	quarter tesseractic honeycomb	q{4,32,4}	or or	h{4,32}	h3{4,32}		{3,4}×{}
qδ6	quarter 5-cubic honeycomb	q{4,33,4}		h{4,33}	h4{4,33}		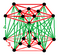Rectified 5-cell antiprism
qδ7	quarter 6-cubic honeycomb	q{4,34,4}		h{4,34}	h5{4,34}	{3,3}×{3,3}
qδ8	quarter 7-cubic honeycomb	q{4,35,4}		h{4,35}	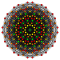h6{4,35}	{3,3}×{3,31,1}
qδ9	quarter 8-cubic honeycomb	q{4,36,4}		h{4,36}	h7{4,36}	{3,3}×{3,32,1} {3,31,1}×{3,31,1}
qδn	quarter n-cubic honeycomb	q{4,3n-3,4}	...	h{4,3n-2}	hn-2{4,3n-2}	...