Rectified 5-cell

Rectified 5-cell
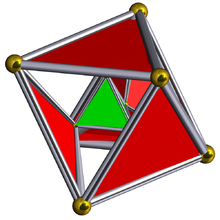Schlegel diagram with the 5 tetrahedral cells shown.
Type	Uniform 4-polytope
Schläfli symbol	t1{3,3,3} or r{3,3,3} {32,1} = ${\displaystyle \left\{{\begin{array}{l}3\\3,3\end{array}}\right\}}$
Coxeter-Dynkin diagram
Cells	10	5 {3,3} 5 3.3.3.3
Faces	30 {3}
Edges	30
Vertices	10
Vertex figure	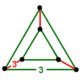Triangular prism
Symmetry group	A4, [3,3,3], order 120
Petrie polygon	Pentagon
Properties	convex, isogonal, isotoxal
Uniform index	1 2 3

In four-dimensional geometry, the rectified 5-cell is a uniform 4-polytope composed of 5 regular tetrahedral and 5 regular octahedral cells. Each edge has one tetrahedron and two octahedra. Each vertex has two tetrahedra and three octahedra. In total it has 30 triangle faces, 30 edges, and 10 vertices. Each vertex is surrounded by 3 octahedra and 2 tetrahedra; the vertex figure is a triangular prism.

Topologically, under its highest symmetry, [3,3,3], there is only one geometrical form, containing 5 regular tetrahedra and 5 rectified tetrahedra (which is geometrically the same as a regular octahedron). It is also topologically identical to a tetrahedron-octahedron segmentochoron.^{[clarification needed]}

The vertex figure of the rectified 5-cell is a uniform triangular prism, formed by three octahedra around the sides, and two tetrahedra on the opposite ends.^[1]

Despite having the same number of vertices as cells (10) and the same number of edges as faces (30), the rectified 5-cell is not self-dual because the vertex figure (a uniform triangular prism) is not a dual of the polychoron's cells.