| Rectified tesseract | ||
|---|---|---|
 Schlegel diagram Centered on cuboctahedron tetrahedral cells shown | ||
| Type | Uniform 4-polytope | |
| Schläfli symbol | r{4,3,3} = 2r{3,31,1} h3{4,3,3} | |
| Coxeter-Dynkin diagrams | ||
| Cells | 24 | 8 (3.4.3.4) 16 (3.3.3) |
| Faces | 88 | 64 {3} 24 {4} |
| Edges | 96 | |
| Vertices | 32 | |
| Vertex figure | 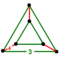 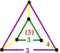 (Elongated equilateral-triangular prism) | |
| Symmetry group | B4 [3,3,4], order 384 D4 [31,1,1], order 192 | |
| Properties | convex, edge-transitive | |
| Uniform index | 10 11 12 | |

In geometry, the rectified tesseract, rectified 8-cell is a uniform 4-polytope (4-dimensional polytope) bounded by 24 cells: 8 cuboctahedra, and 16 tetrahedra. It has half the vertices of a runcinated tesseract, with its ![]()
![]()
![]()
![]()
![]()
![]()
![]() construction, called a runcic tesseract.
construction, called a runcic tesseract.
It has two uniform constructions, as a rectified 8-cell r{4,3,3} and a cantellated demitesseract, rr{3,31,1}, the second alternating with two types of tetrahedral cells.
E. L. Elte identified it in 1912 as a semiregular polytope, labeling it as tC8.
