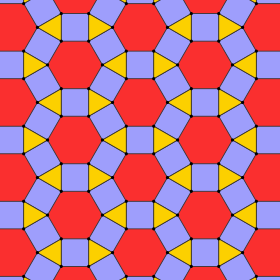
Rhombitrihexagonal tiling

Rhombitrihexagonal tiling
Type	Semiregular tiling
Vertex configuration	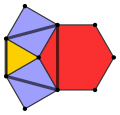3.4.6.4
Schläfli symbol	rr{6,3} or ${\displaystyle r{\begin{Bmatrix}6\\3\end{Bmatrix}}}$
Wythoff symbol	3 | 6 2
Coxeter diagram
Symmetry	p6m, [6,3], (*632)
Rotation symmetry	p6, [6,3]+, (632)
Bowers acronym	Rothat
Dual	Deltoidal trihexagonal tiling
Properties	Vertex-transitive

In geometry, the rhombitrihexagonal tiling is a semiregular tiling of the Euclidean plane. There are one triangle, two squares, and one hexagon on each vertex. It has Schläfli symbol of rr{3,6}.

John Conway calls it a rhombihexadeltille.^[1] It can be considered a cantellated by Norman Johnson's terminology or an expanded hexagonal tiling by Alicia Boole Stott's operational language.

There are three regular and eight semiregular tilings in the plane.