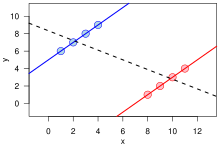

Simpson's paradox is a phenomenon in probability and statistics in which a trend appears in several groups of data but disappears or reverses when the groups are combined. This result is often encountered in social-science and medical-science statistics,[1][2][3] and is particularly problematic when frequency data are unduly given causal interpretations.[4] The paradox can be resolved when confounding variables and causal relations are appropriately addressed in the statistical modeling[4][5] (e.g., through cluster analysis[6]).
Simpson's paradox has been used to illustrate the kind of misleading results that the misuse of statistics can generate.[7][8]
Edward H. Simpson first described this phenomenon in a technical paper in 1951,[9] but the statisticians Karl Pearson (in 1899[10]) and Udny Yule (in 1903[11]) had mentioned similar effects earlier. The name Simpson's paradox was introduced by Colin R. Blyth in 1972.[12] It is also referred to as Simpson's reversal, the Yule–Simpson effect, the amalgamation paradox, or the reversal paradox.[13]
Mathematician Jordan Ellenberg argues that Simpson's paradox is misnamed as "there's no contradiction involved, just two different ways to think about the same data" and suggests that its lesson "isn't really to tell us which viewpoint to take but to insist that we keep both the parts and the whole in mind at once."[14]
- ^ Clifford H. Wagner (February 1982). "Simpson's Paradox in Real Life". The American Statistician. 36 (1): 46–48. doi:10.2307/2684093. JSTOR 2684093.
- ^ Holt, G. B. (2016). Potential Simpson's paradox in multicenter study of intraperitoneal chemotherapy for ovarian cancer. Journal of Clinical Oncology, 34(9), 1016–1016.
- ^ Franks, Alexander; Airoldi, Edoardo; Slavov, Nikolai (2017). "Post-transcriptional regulation across human tissues". PLOS Computational Biology. 13 (5): e1005535. arXiv:1506.00219. Bibcode:2017PLSCB..13E5535F. doi:10.1371/journal.pcbi.1005535. ISSN 1553-7358. PMC 5440056. PMID 28481885.
- ^ a b Judea Pearl. Causality: Models, Reasoning, and Inference, Cambridge University Press (2000, 2nd edition 2009). ISBN 0-521-77362-8.
- ^ Kock, N., & Gaskins, L. (2016). Simpson's paradox, moderation and the emergence of quadratic relationships in path models: An information systems illustration. International Journal of Applied Nonlinear Science, 2(3), 200–234.
- ^ Rogier A. Kievit, Willem E. Frankenhuis, Lourens J. Waldorp and Denny Borsboom, Simpson's paradox in psychological science: a practical guide https://doi.org/10.3389/fpsyg.2013.00513
- ^ Robert L. Wardrop (February 1995). "Simpson's Paradox and the Hot Hand in Basketball". The American Statistician, 49 (1): pp. 24–28.
- ^ Alan Agresti (2002). "Categorical Data Analysis" (Second edition). John Wiley and Sons ISBN 0-471-36093-7
- ^ Simpson, Edward H. (1951). "The Interpretation of Interaction in Contingency Tables". Journal of the Royal Statistical Society, Series B. 13 (2): 238–241. doi:10.1111/j.2517-6161.1951.tb00088.x.
- ^ Pearson, Karl; Lee, Alice; Bramley-Moore, Lesley (1899). "Genetic (reproductive) selection: Inheritance of fertility in man, and of fecundity in thoroughbred racehorses". Philosophical Transactions of the Royal Society A. 192: 257–330. doi:10.1098/rsta.1899.0006.
- ^ G. U. Yule (1903). "Notes on the Theory of Association of Attributes in Statistics". Biometrika. 2 (2): 121–134. doi:10.1093/biomet/2.2.121.
- ^ Colin R. Blyth (June 1972). "On Simpson's Paradox and the Sure-Thing Principle". Journal of the American Statistical Association. 67 (338): 364–366. doi:10.2307/2284382. JSTOR 2284382.
- ^ I. J. Good, Y. Mittal (June 1987). "The Amalgamation and Geometry of Two-by-Two Contingency Tables". The Annals of Statistics. 15 (2): 694–711. doi:10.1214/aos/1176350369. ISSN 0090-5364. JSTOR 2241334.
- ^ Ellenberg, Jordan (May 25, 2021). Shape: The Hidden Geometry of Information, Biology, Strategy, Democracy and Everything Else. New York: Penguin Press. p. 228. ISBN 978-1-9848-7905-9. OCLC 1226171979.