Square lattice

Square lattices
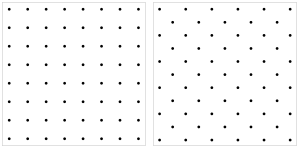
Upright square
Simple 		diagonal square
Centered
Upright square tiling. The vertices of all squares together with their centers form an upright square lattice. For each color the centers of the squares of that color form a diagonal square lattice which is in linear scale √2 times as large as the upright square lattice.

In mathematics, the square lattice is a type of lattice in a two-dimensional Euclidean space. It is the two-dimensional version of the integer lattice, denoted as ⁠⁠.[1] It is one of the five types of two-dimensional lattices as classified by their symmetry groups;[2] its symmetry group in IUC notation as p4m,[3] Coxeter notation as [4,4],[4] and orbifold notation as *442.[5]

Two orientations of an image of the lattice are by far the most common. They can conveniently be referred to as the upright square lattice and diagonal square lattice; the latter is also called the centered square lattice.[6] They differ by an angle of 45°. This is related to the fact that a square lattice can be partitioned into two square sub-lattices, as is evident in the colouring of a checkerboard.

  1. ^ Conway, John; Sloane, Neil J. A. (1999), Sphere Packings, Lattices and Groups, Springer, p. 106, ISBN 9780387985855.
  2. ^ Golubitsky, Martin; Stewart, Ian (2003), The Symmetry Perspective: From Equilibrium to Chaos in Phase Space and Physical Space, Progress in Mathematics, vol. 200, Springer, p. 129, ISBN 9783764321710.
  3. ^ Field, Michael; Golubitsky, Martin (2009), Symmetry in Chaos: A Search for Pattern in Mathematics, Art, and Nature (2nd ed.), SIAM, p. 47, ISBN 9780898717709.
  4. ^ Johnson, Norman W.; Weiss, Asia Ivić (1999), "Quadratic integers and Coxeter groups", Canadian Journal of Mathematics, 51 (6): 1307–1336, doi:10.4153/CJM-1999-060-6. See in particular the top of p. 1320.
  5. ^ Schattschneider, Doris; Senechal, Marjorie (2004), "Tilings", in Goodman, Jacob E.; O'Rourke, Joseph (eds.), Handbook of Discrete and Computational Geometry, Discrete Mathematics and Its Applications (2nd ed.), CRC Press, pp. 53–72, ISBN 9781420035315. See in particular the table on p. 62 relating IUC notation to orbifold notation.
  6. ^ Johnston, Bernard L.; Richman, Fred (1997), Numbers and Symmetry: An Introduction to Algebra, CRC Press, p. 159, ISBN 9780849303012.