|
Probability density function 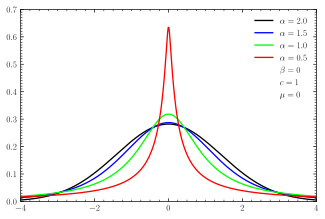 Symmetric -stable distributions with unit scale factor  Skewed centered stable distributions with unit scale factor | |||
|
Cumulative distribution function 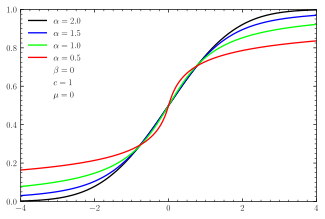 CDFs for symmetric -stable distributions 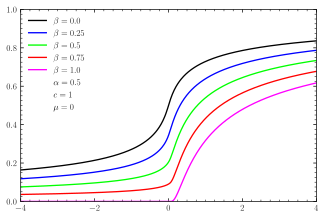 CDFs for skewed centered stable distributions | |||
| Parameters |
— stability parameter | ||
|---|---|---|---|
| Support |
x ∈ [μ, +∞) if and x ∈ (-∞, μ] if and x ∈ R otherwise | ||
| not analytically expressible, except for some parameter values | |||
| CDF | not analytically expressible, except for certain parameter values | ||
| Mean | μ when , otherwise undefined | ||
| Median | μ when , otherwise not analytically expressible | ||
| Mode | μ when , otherwise not analytically expressible | ||
| Variance | 2c2 when , otherwise infinite | ||
| Skewness | 0 when , otherwise undefined | ||
| Excess kurtosis | 0 when , otherwise undefined | ||
| Entropy | not analytically expressible, except for certain parameter values | ||
| MGF |
when , when , when , otherwise undefined | ||
| CF |
| ||
In probability theory, a distribution is said to be stable if a linear combination of two independent random variables with this distribution has the same distribution, up to location and scale parameters. A random variable is said to be stable if its distribution is stable. The stable distribution family is also sometimes referred to as the Lévy alpha-stable distribution, after Paul Lévy, the first mathematician to have studied it.[1][2]
Of the four parameters defining the family, most attention has been focused on the stability parameter, (see panel). Stable distributions have , with the upper bound corresponding to the normal distribution, and to the Cauchy distribution. The distributions have undefined variance for , and undefined mean for . The importance of stable probability distributions is that they are "attractors" for properly normed sums of independent and identically distributed (iid) random variables. The normal distribution defines a family of stable distributions. By the classical central limit theorem the properly normed sum of a set of random variables, each with finite variance, will tend toward a normal distribution as the number of variables increases. Without the finite variance assumption, the limit may be a stable distribution that is not normal. Mandelbrot referred to such distributions as "stable Paretian distributions",[3][4][5] after Vilfredo Pareto. In particular, he referred to those maximally skewed in the positive direction with as "Pareto–Lévy distributions",[1] which he regarded as better descriptions of stock and commodity prices than normal distributions.[6]
- ^ a b Mandelbrot, B. (1960). "The Pareto–Lévy Law and the Distribution of Income". International Economic Review. 1 (2): 79–106. doi:10.2307/2525289. JSTOR 2525289.
- ^ Lévy, Paul (1925). Calcul des probabilités. Paris: Gauthier-Villars. OCLC 1417531.
- ^ Mandelbrot, B. (1961). "Stable Paretian Random Functions and the Multiplicative Variation of Income". Econometrica. 29 (4): 517–543. doi:10.2307/1911802. JSTOR 1911802.
- ^ Mandelbrot, B. (1963). "The Variation of Certain Speculative Prices". The Journal of Business. 36 (4): 394–419. doi:10.1086/294632. JSTOR 2350970.
- ^ Fama, Eugene F. (1963). "Mandelbrot and the Stable Paretian Hypothesis". The Journal of Business. 36 (4): 420–429. doi:10.1086/294633. JSTOR 2350971.
- ^ Mandelbrot, B. (1963). "New methods in statistical economics". The Journal of Political Economy. 71 (5): 421–440. doi:10.1086/258792. S2CID 53004476.

![{\displaystyle \alpha \in (0,2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98dade01a06507996c8330ec68b7c0f7bc305a05)












![{\displaystyle \exp \!{\Big [}\;it\mu -|c\,t|^{\alpha }\,(1-i\beta \operatorname {sgn}(t)\Phi )\;{\Big ]},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d98d0e47ac7b119c61fcddb23c16046f082f0b5)





