Student's t-distribution

Student's $t$
	Probability density function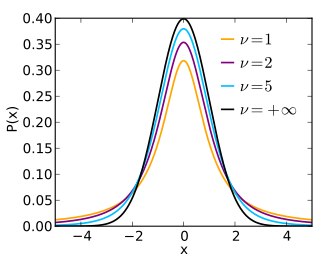
	Cumulative distribution function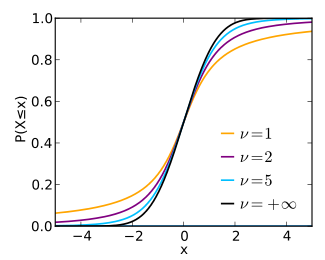
Parameters	degrees of freedom (real, almost always a positive integer)
Support
PDF
CDF	; where is the hypergeometric function
Mean	for otherwise undefined
Median
Mode
Variance	for ∞ for ; otherwise undefined
Skewness	for otherwise undefined
Excess kurtosis	for ∞ for ; otherwise undefined
Entropy	; where is the digamma function, is the beta function.
MGF	undefined
CF	for is the modified Bessel function of the second kind;
Expected shortfall	Where is the inverse standardized Student t CDF, and is the standardized Student t PDF.

In probability theory and statistics, Student's $t$ distribution (or simply the $t$ distribution) $\ t_{\nu }\$ is a continuous probability distribution that generalizes the standard normal distribution. Like the latter, it is symmetric around zero and bell-shaped.

However, $\ t_{\nu }\$ has heavier tails and the amount of probability mass in the tails is controlled by the parameter $\ \nu ~~.$ For $\ \nu =1\$ the Student's $t$ distribution $t_{\nu }$ becomes the standard Cauchy distribution, which has very "fat" tails; whereas for $\ \nu \rightarrow \infty \$ it becomes the standard normal distribution $\ {\mathcal {N}}(0,1)\,$ which has very "thin" tails.

The Student's $t$ distribution plays a role in a number of widely used statistical analyses, including Student's $t$ test for assessing the statistical significance of the difference between two sample means, the construction of confidence intervals for the difference between two population means, and in linear regression analysis.

In the form of the location-scale $t$ distribution $lst(\mu ,\tau ^{2},\nu )$ it generalizes the normal distribution and also arises in the Bayesian analysis of data from a normal family as a compound distribution when marginalizing over the variance parameter.

^ Hurst, Simon. "The characteristic function of the Student $t$ distribution". Financial Mathematics Research Report. Statistics Research Report No. SRR044-95. Archived from the original on February 18, 2010.
^ Norton, Matthew; Khokhlov, Valentyn; Uryasev, Stan (2019). "Calculating CVaR and bPOE for common probability distributions with application to portfolio optimization and density estimation" (PDF). Annals of Operations Research. 299 (1–2). Springer: 1281–1315. arXiv:1811.11301. doi:10.1007/s10479-019-03373-1. S2CID 254231768. Retrieved 2023-02-27.

[1] Hurst, Simon. "The characteristic function of the Student $t$ distribution". Financial Mathematics Research Report. Statistics Research Report No. SRR044-95. Archived from the original on February 18, 2010.

[norton-2] Norton, Matthew; Khokhlov, Valentyn; Uryasev, Stan (2019). "Calculating CVaR and bPOE for common probability distributions with application to portfolio optimization and density estimation" (PDF). Annals of Operations Research. 299 (1–2). Springer: 1281–1315. arXiv:1811.11301. doi:10.1007/s10479-019-03373-1. S2CID 254231768. Retrieved 2023-02-27.

[1]

[2]

Student's $t$
Probability density function
Cumulative distribution function
Parameters	$\ \nu >0\$ degrees of freedom (real, almost always a positive integer)
Support	$\ x\in (-\infty ,\infty )$
PDF	$\textstyle \ {\frac {\Gamma \left({\frac {\ \nu +1\ }{2}}\right)}{{\sqrt {\pi \ \nu \ }}\ \Gamma \left({\frac {\nu }{\ 2\ }}\right)}}\ \left(\ 1+{\frac {~x^{2}\ }{\nu }}\ \right)^{-{\frac {\ \nu +1\ }{2}}}\$
CDF	${\begin{matrix}\ {\frac {\ 1\ }{2}}+x\ \Gamma \left({\frac {\ \nu +1\ }{2}}\right)\times \\[0.5em]{\frac {\ {{}_{2}F_{1}}\!\left(\ {\frac {\ 1\ }{2}},\ {\frac {\ \nu +1\ }{2}};\ {\frac {3}{\ 2\ }};\ -{\frac {~x^{2}\ }{\nu }}\ \right)\ }{\ {\sqrt {\pi \nu }}\ \Gamma \left({\frac {\ \nu \ }{2}}\right)\ }}\ ,\end{matrix}}$ where $\ {}_{2}F_{1}\!(\ ,\ ;\ ;\ )\$ is the hypergeometric function
Mean	$\ 0\$ for $\ \nu >1\ ,$ otherwise undefined
Median	$\ 0\$
Mode	$\ 0\$
Variance	$\textstyle \ {\frac {\nu }{\ \nu -2\ }}\$ for $\ \nu >2\ ,$ $\infty$ for $\ 1<\nu \leq 2\ ,$ otherwise undefined
Skewness	$\ 0\$ for $\ \nu >3\ ,$ otherwise undefined
Excess kurtosis	$\textstyle \ {\frac {6}{\ \nu -4\ }}$ for $\ \nu >4\ ,$ ∞ for $\ 2<\nu \leq 4\ ,$ otherwise undefined
Entropy	$\ {\begin{matrix}{\frac {\ \nu +1\ }{2}}\left[\ \psi \left({\frac {\ \nu +1\ }{2}}\right)-\psi \left({\frac {\ \nu \ }{2}}\right)\ \right]\\[0.5em]+\ln \left[{\sqrt {\nu \ }}\ {\mathrm {B} }\left(\ {\frac {\ \nu \ }{2}},\ {\frac {\ 1\ }{2}}\ \right)\right]\ {\scriptstyle {\text{(nats)}}}\ \end{matrix}}$ where $\psi ()\$ is the digamma function, $\ {\mathrm {B} }(\ ,\ )\$ is the beta function.
MGF	undefined
CF	$\textstyle {\frac {\ \left(\ {\sqrt {\nu \ }}\ \|t\|\ \right)^{\nu /2}\ K_{\nu /2}\left(\ {\sqrt {\nu \ }}\ \|t\|\ \right)\ }{\ \Gamma (\nu /2)\ 2^{\nu /2-1}\ }}\$ for $\ \nu >0\$ $\ K_{\nu }(x)\$ is the modified Bessel function of the second kind^[1]
Expected shortfall	$\ \mu +s\ \left(\ {\frac {\ \nu +T^{-1}(1-p)^{2}\ \times \ \tau \left(T^{-1}(1-p)^{2}\right)\ }{\ (\nu -1)(1-p)\ }}\ \right)\$ Where $\ T^{-1}(\ )\$ is the inverse standardized Student $t$ CDF, and $\ \tau (\ )\$ is the standardized Student t PDF.^[2]