Superior highly composite number

Divisor function $d (n)$ up to $n = 250$

In number theory, a superior highly composite number is a natural number which, in a particular rigorous sense, has many divisors. Particularly, it is defined by a ratio between the number of divisors an integer has and that integer raised to some positive power.

For any possible exponent, whichever integer has the greatest ratio is a superior highly composite number. It is a stronger restriction than that of a highly composite number, which is defined as having more divisors than any smaller positive integer.

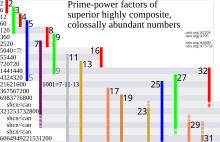
The first ten superior highly composite numbers and their factorization are listed.

# prime factors	SHCN $n$	Prime factorization	Prime exponents	# divisors $d (n)$	Primorial factorization
1	2	$2$	1	2	$2$
2	6	$2 \cdot 3$	1,1	4	$6$
3	12	$22 \cdot 3$	2,1	6	$2 \cdot 6$
4	60	$22 \cdot 3 \cdot 5$	2,1,1	12	$2 \cdot 30$
5	120	$23 \cdot 3 \cdot 5$	3,1,1	16	$22 \cdot 30$
6	360	$23 \cdot 3 2 \cdot 5$	3,2,1	24	$2 \cdot 6 \cdot 30$
7	2520	$23 \cdot 3 2 \cdot 5 \cdot 7$	3,2,1,1	48	$2 \cdot 6 \cdot 210$
8	5040	$24 \cdot 3 2 \cdot 5 \cdot 7$	4,2,1,1	60	$22 \cdot 6 \cdot 210$
9	55440	$24 \cdot 3 2 \cdot 5 \cdot 7 \cdot 11$	4,2,1,1,1	120	$22 \cdot 6 \cdot 2310$
10	720720	$24 \cdot 3 2 \cdot 5 \cdot 7 \cdot 11 \cdot 13$	4,2,1,1,1,1	240	$22 \cdot 6 \cdot 30030$

For a superior highly composite number $n$ there exists a positive real number $ε > 0$ such that for all natural numbers $k > 1$ we have ${\frac {d(n)}{n^{\varepsilon }}}\geq {\frac {d(k)}{k^{\varepsilon }}}$ where $d (n)$ , the divisor function, denotes the number of divisors of $n$ . The term was coined by Ramanujan (1915).^[1]

For example, the number with the most divisors per square root of the number itself is 12; this can be demonstrated using some highly composites near 12. ${\frac {2}{2^{.5}}}\approx 1.414,{\frac {3}{4^{.5}}}=1.5,{\frac {4}{6^{.5}}}\approx 1.633,{\frac {6}{12^{.5}}}\approx 1.732,{\frac {8}{24^{.5}}}\approx 1.633,{\frac {12}{60^{.5}}}\approx 1.549$

120 is another superior highly composite number because it has the highest ratio of divisors to itself raised to the .4 power. ${\frac {9}{36^{.4}}}\approx 2.146,{\frac {10}{48^{.4}}}\approx 2.126,{\frac {12}{60^{.4}}}\approx 2.333,{\frac {16}{120^{.4}}}\approx 2.357,{\frac {18}{180^{.4}}}\approx 2.255,{\frac {20}{240^{.4}}}\approx 2.233,{\frac {24}{360^{.4}}}\approx 2.279$

The first 15 superior highly composite numbers, 2, 6, 12, 60, 120, 360, 2520, 5040, 55440, 720720, 1441440, 4324320, 21621600, 367567200, 6983776800 (sequence A002201 in the OEIS) are also the first 15 colossally abundant numbers, which meet a similar condition based on the sum-of-divisors function rather than the number of divisors. Neither set, however, is a subset of the other.

^ Weisstein, Eric W. "Superior Highly Composite Number". mathworld.wolfram.com. Retrieved 2021-03-05.

[1] Weisstein, Eric W. "Superior Highly Composite Number". mathworld.wolfram.com. Retrieved 2021-03-05.

[1]