| Tetrakis hexahedron | |
|---|---|
 (Click here for rotating model) | |
| Type | Catalan solid |
| Coxeter diagram | |
| Conway notation | kC |
| Face type | V4.6.6 isosceles triangle |
| Faces | 24 |
| Edges | 36 |
| Vertices | 14 |
| Vertices by type | 6{4}+8{6} |
| Symmetry group | Oh, B3, [4,3], (*432) |
| Rotation group | O, [4,3]+, (432) |
| Dihedral angle | 143°07′48″ arccos(−4/5) |
| Properties | convex, face-transitive |
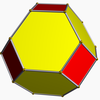 Truncated octahedron (dual polyhedron) |
 Net |
Dual compound of truncated octahedron and tetrakis hexahedron. The woodcut on the left is from Perspectiva Corporum Regularium (1568) by Wenzel Jamnitzer.
Die and crystal model
Drawing and crystal model of variant with tetrahedral symmetry called hexakis tetrahedron [1]
In geometry, a tetrakis hexahedron (also known as a tetrahexahedron, hextetrahedron, tetrakis cube, and kiscube[2]) is a Catalan solid. Its dual is the truncated octahedron, an Archimedean solid.
It can be called a disdyakis hexahedron or hexakis tetrahedron as the dual of an omnitruncated tetrahedron, and as the barycentric subdivision of a tetrahedron.[3]
- ^ Hexakistetraeder in German, see e.g. Meyers page and Brockhaus page. The same drawing appears in Brockhaus and Efron as преломленный пирамидальный тетраэдр (refracted pyramidal tetrahedron).
- ^ Conway, Symmetries of Things, p.284
- ^ Langer, Joel C.; Singer, David A. (2010), "Reflections on the lemniscate of Bernoulli: the forty-eight faces of a mathematical gem", Milan Journal of Mathematics, 78 (2): 643–682, doi:10.1007/s00032-010-0124-5, MR 2781856






