Triakis tetrahedron

Triakis tetrahedron
(Click here for rotating model)
Type	Catalan solid
Coxeter diagram
Conway notation	kT
Face type	V3.6.6 isosceles triangle
Faces	12
Edges	18
Vertices	8
Vertices by type	4{3}+4{6}
Symmetry group	Td, A3, [3,3], (*332)
Rotation group	T, [3,3]+, (332)
Dihedral angle	129°31′16″ arccos(−⁠7/11⁠)
Properties	convex, face-transitive
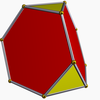Truncated tetrahedron (dual polyhedron)	Net

In geometry, a triakis tetrahedron (or kistetrahedron^[1]) is a Catalan solid with 12 faces. Each Catalan solid is the dual of an Archimedean solid. The dual of the triakis tetrahedron is the truncated tetrahedron.

The triakis tetrahedron can be seen as a tetrahedron with a triangular pyramid added to each face; that is, it is the Kleetope of the tetrahedron. It is very similar to the net for the 5-cell, as the net for a tetrahedron is a triangle with other triangles added to each edge, the net for the 5-cell a tetrahedron with pyramids attached to each face. This interpretation is expressed in the name.

The length of the shorter edges is ⁠3/5⁠ that of the longer edges.^[2] The area, A, and volume, V, of the triakis tetrahedron, with shorter edge length "a", is equal to

A = ⁠5/3⁠√11 V = ⁠25/36⁠√2.