| Transitive binary relations | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
All definitions tacitly require the homogeneous relation be transitive: for all if and then |

I) representation as a strict weak order where is shown as an arrow from to ;
II) representation as a total preorder , shown using arrows;
III) representation as an ordered partition, with the sets of the partition as dotted ellipses and the total order on these sets shown with arrows.
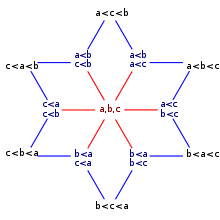
In mathematics, especially order theory, a weak ordering is a mathematical formalization of the intuitive notion of a ranking of a set, some of whose members may be tied with each other. Weak orders are a generalization of totally ordered sets (rankings without ties) and are in turn generalized by (strictly) partially ordered sets and preorders.[1]
There are several common ways of formalizing weak orderings, that are different from each other but cryptomorphic (interconvertable with no loss of information): they may be axiomatized as strict weak orderings (strictly partially ordered sets in which incomparability is a transitive relation), as total preorders (transitive binary relations in which at least one of the two possible relations exists between every pair of elements), or as ordered partitions (partitions of the elements into disjoint subsets, together with a total order on the subsets). In many cases another representation called a preferential arrangement based on a utility function is also possible.
Weak orderings are counted by the ordered Bell numbers. They are used in computer science as part of partition refinement algorithms, and in the C++ Standard Library.[2]
- ^ Roberts, Fred; Tesman, Barry (2011), Applied Combinatorics (2nd ed.), CRC Press, Section 4.2.4 Weak Orders, pp. 254–256, ISBN 9781420099836.
- ^ Josuttis, Nicolai M. (2012), The C++ Standard Library: A Tutorial and Reference, Addison-Wesley, p. 469, ISBN 9780132977739.


























